The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources -
Examples
 Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot - References
The following sections provide information about the families of parametric distributions that you can fit with the HISTOGRAM statement. Properties of these distributions are discussed by Johnson, Kotz, and Balakrishnan (1994, 1995).
The fitted density function is
where ![]() and
and
-
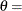 lower threshold parameter (lower endpoint parameter)
lower threshold parameter (lower endpoint parameter)
-
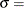 scale parameter
scale parameter 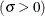
-
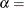 shape parameter
shape parameter 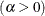
-
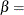 shape parameter
shape parameter 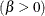
-
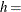 width of histogram interval
width of histogram interval
-
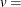 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
Note: This notation is consistent with that of other distributions that you can fit with the HISTOGRAM statement. However, many texts, including Johnson, Kotz, and Balakrishnan (1995), write the beta density function as
The two parameterizations are related as follows:
The range of the beta distribution is bounded below by a threshold parameter ![]() and above by
and above by ![]() . If you specify a fitted beta curve by using the BETA option,
. If you specify a fitted beta curve by using the BETA option, ![]() must be less than the minimum data value and
must be less than the minimum data value and ![]() must be greater than the maximum data value. You can specify
must be greater than the maximum data value. You can specify ![]() and
and ![]() with the THETA= and SIGMA= beta-options in parentheses after the keyword BETA. By default,
with the THETA= and SIGMA= beta-options in parentheses after the keyword BETA. By default, ![]() and
and ![]() . If you specify THETA=EST and SIGMA=EST, maximum likelihood estimates are computed for
. If you specify THETA=EST and SIGMA=EST, maximum likelihood estimates are computed for ![]() and
and ![]() . However, three- and four-parameter maximum likelihood estimation does not always converge.
. However, three- and four-parameter maximum likelihood estimation does not always converge.
In addition, you can specify ![]() and
and ![]() with the ALPHA= and BETA= beta-options, respectively. By default, the procedure calculates maximum likelihood estimates for
with the ALPHA= and BETA= beta-options, respectively. By default, the procedure calculates maximum likelihood estimates for ![]() and
and ![]() . For example, to fit a beta density curve to a set of data bounded below by 32 and above by 212 with maximum likelihood estimates
for
. For example, to fit a beta density curve to a set of data bounded below by 32 and above by 212 with maximum likelihood estimates
for ![]() and
and ![]() , use the following statement:
, use the following statement:
histogram Length / beta(theta=32 sigma=180);
The beta distributions are also referred to as Pearson Type I or II distributions. These include the power function distribution
(![]() ), the arc sine distribution (
), the arc sine distribution (![]() ), and the generalized arc sine distributions (
), and the generalized arc sine distributions (![]() ,
, ![]() ).
).
You can use the DATA step function QUANTILE to compute beta quantiles and the DATA step function CDF to compute beta probabilities.
The fitted density function is
where
-
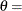 threshold parameter
threshold parameter
-
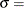 scale parameter
scale parameter 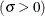
-
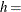 width of histogram interval
width of histogram interval
-
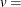 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
The threshold parameter ![]() must be less than or equal to the minimum data value. You can specify
must be less than or equal to the minimum data value. You can specify ![]() with the THRESHOLD= exponential-option. By default,
with the THRESHOLD= exponential-option. By default, ![]() . If you specify THETA=EST, a maximum likelihood estimate is computed for
. If you specify THETA=EST, a maximum likelihood estimate is computed for ![]() . In addition, you can specify
. In addition, you can specify ![]() with the SCALE= exponential-option. By default, the procedure calculates a maximum likelihood estimate for
with the SCALE= exponential-option. By default, the procedure calculates a maximum likelihood estimate for ![]() . Note that some authors define the scale parameter as
. Note that some authors define the scale parameter as ![]() .
.
The exponential distribution is a special case of both the gamma distribution (with ![]() ) and the Weibull distribution (with
) and the Weibull distribution (with ![]() ). A related distribution is the extreme value distribution. If
). A related distribution is the extreme value distribution. If ![]() has an exponential distribution, then X has an extreme value distribution.
has an exponential distribution, then X has an extreme value distribution.
You can use the DATA step function QUANTILE to compute exponential quantiles and the DATA step function CDF to compute exponential probabilities.
The fitted density function is
where
-
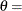 threshold parameter
threshold parameter
-
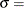 scale parameter
scale parameter 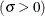
-
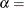 shape parameter
shape parameter 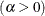
-
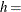 width of histogram interval
width of histogram interval
-
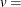 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
The threshold parameter ![]() must be less than the minimum data value. You can specify
must be less than the minimum data value. You can specify ![]() with the THRESHOLD= gamma-option. By default,
with the THRESHOLD= gamma-option. By default, ![]() . If you specify THETA=EST, a maximum likelihood estimate is computed for
. If you specify THETA=EST, a maximum likelihood estimate is computed for ![]() . In addition, you can specify
. In addition, you can specify ![]() and
and ![]() with the SCALE= and ALPHA= gamma-options. By default, the procedure calculates maximum likelihood estimates for
with the SCALE= and ALPHA= gamma-options. By default, the procedure calculates maximum likelihood estimates for ![]() and
and ![]() .
.
The gamma distributions are also referred to as Pearson Type III distributions, and they include the chi-square, exponential, and Erlang distributions. The probability density function for the chi-square distribution is
Notice that this is a gamma distribution with ![]() ,
, ![]() , and
, and ![]() . The exponential distribution is a gamma distribution with
. The exponential distribution is a gamma distribution with ![]() , and the Erlang distribution is a gamma distribution with
, and the Erlang distribution is a gamma distribution with ![]() being a positive integer. A related distribution is the Rayleigh distribution. If
being a positive integer. A related distribution is the Rayleigh distribution. If ![]() where the
where the ![]() ’s are independent
’s are independent ![]() variables, then
variables, then ![]() is distributed with a
is distributed with a ![]() distribution having a probability density function of
distribution having a probability density function of
If ![]() , the preceding distribution is referred to as the Rayleigh distribution.
, the preceding distribution is referred to as the Rayleigh distribution.
You can use the DATA step function QUANTILE to compute gamma quantiles and the DATA step function CDF to compute gamma probabilities.
The fitted density function is
where
-
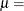 location parameter
location parameter
-
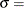 scale parameter
scale parameter 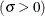
-
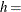 width of histogram interval
width of histogram interval
-
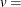 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
You can specify ![]() and
and ![]() with the MU= and SIGMA= Gumbel-options, respectively. By default, the procedure calculates maximum likelihood estimates for these parameters.
with the MU= and SIGMA= Gumbel-options, respectively. By default, the procedure calculates maximum likelihood estimates for these parameters.
Note: The Gumbel distribution is also referred to as Type 1 extreme value distribution.
Note: The random variable X has Gumbel (Type 1 extreme value) distribution if and only if ![]() has Weibull distribution and
has Weibull distribution and ![]() has standard exponential distribution.
has standard exponential distribution.
The fitted density function is
where
-
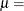 location parameter
location parameter 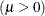
-
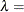 shape parameter
shape parameter 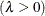
-
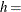 width of histogram interval
width of histogram interval
-
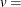 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
The location parameter ![]() has to be greater then zero. You can specify
has to be greater then zero. You can specify ![]() with the MU= iGauss-option. In addition, you can specify shape parameter
with the MU= iGauss-option. In addition, you can specify shape parameter ![]() with LAMBDA= iGauss-option. By default, the procedure calculates maximum likelihood estimates for
with LAMBDA= iGauss-option. By default, the procedure calculates maximum likelihood estimates for ![]() and
and ![]() .
.
Note: The special case where ![]() and
and ![]() corresponds to the Wald distribution.
corresponds to the Wald distribution.
You can use the DATA step function QUANTILE to compute inverse Gaussian quantiles and the DATA step function CDF to compute inverse Gaussian probabilities.
The fitted density function is
where
-
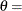 threshold parameter
threshold parameter
-
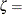 scale parameter
scale parameter 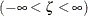
-
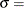 shape parameter
shape parameter 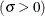
-
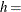 width of histogram interval
width of histogram interval
-
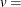 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
The threshold parameter ![]() must be less than the minimum data value. You can specify
must be less than the minimum data value. You can specify ![]() with the THRESHOLD= lognormal-option. By default,
with the THRESHOLD= lognormal-option. By default, ![]() . If you specify THETA=EST, a maximum likelihood estimate is computed for
. If you specify THETA=EST, a maximum likelihood estimate is computed for ![]() . You can specify
. You can specify ![]() and
and ![]() with the SCALE= and SHAPE= lognormal-options, respectively. By default, the procedure calculates maximum likelihood estimates for these parameters.
with the SCALE= and SHAPE= lognormal-options, respectively. By default, the procedure calculates maximum likelihood estimates for these parameters.
Note: The lognormal distribution is also referred to as the ![]() distribution in the Johnson system of distributions.
distribution in the Johnson system of distributions.
Note: This book uses ![]() to denote the shape parameter of the lognormal distribution, whereas
to denote the shape parameter of the lognormal distribution, whereas ![]() is used to denote the scale parameter of the other distributions. The use of
is used to denote the scale parameter of the other distributions. The use of ![]() to denote the lognormal shape parameter is based on the fact that
to denote the lognormal shape parameter is based on the fact that ![]() has a standard normal distribution if X is lognormally distributed. Based on this relationship, you can use the DATA step function PROBIT to compute lognormal quantiles
and the DATA step function PROBNORM to compute probabilities.
has a standard normal distribution if X is lognormally distributed. Based on this relationship, you can use the DATA step function PROBIT to compute lognormal quantiles
and the DATA step function PROBNORM to compute probabilities.
The fitted density function is
where
-
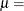 mean
mean
-
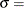 standard deviation
standard deviation 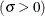
-
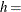 width of histogram interval
width of histogram interval
-
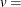 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
You can specify ![]() and
and ![]() with the MU= and SIGMA= normal-options, respectively. By default, the procedure estimates
with the MU= and SIGMA= normal-options, respectively. By default, the procedure estimates ![]() with the sample mean and
with the sample mean and ![]() with the sample standard deviation.
with the sample standard deviation.
You can use the DATA step function QUANTILE to compute beta quantiles and the DATA step function CDF to compute normal probabilities.
Note: The normal distribution is also referred to as the ![]() distribution in the Johnson system of distributions.
distribution in the Johnson system of distributions.
The fitted density function is
where
-
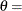 threshold parameter
threshold parameter
-
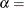 shape parameter
shape parameter
-
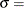 shape parameter
shape parameter 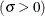
-
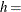 width of histogram interval
width of histogram interval
-
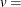 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
The support of the distribution is ![]() for
for ![]() and
and ![]() for
for ![]() .
.
Note: Special cases of Pareto distribution with ![]() and
and ![]() correspond respectively to the exponential distribution with mean
correspond respectively to the exponential distribution with mean ![]() and uniform distribution on the interval
and uniform distribution on the interval ![]() .
.
The threshold parameter ![]() must be less than the minimum data value. You can specify
must be less than the minimum data value. You can specify ![]() with the THETA= Pareto-option. By default,
with the THETA= Pareto-option. By default, ![]() . You can also specify
. You can also specify ![]() and
and ![]() with the ALPHA= and SIGMA= Pareto-options,respectively. By default, the procedure calculates maximum likelihood estimates for these parameters.
with the ALPHA= and SIGMA= Pareto-options,respectively. By default, the procedure calculates maximum likelihood estimates for these parameters.
Note: Maximum likelihood estimation of the parameters works well if ![]() , but not otherwise. In this case the estimators are asymptotically normal and asymptotically efficient. The asymptotic normal
distribution of the maximum likelihood estimates has mean
, but not otherwise. In this case the estimators are asymptotically normal and asymptotically efficient. The asymptotic normal
distribution of the maximum likelihood estimates has mean ![]() and variance-covariance matrix
and variance-covariance matrix
Note: If no local minimum found in the space
there is no maximum likelihood estimator. More details on how to find maximum likelihood estimators and suggested algorithm can be found in Grimshaw(1993).
The fitted density function is
where
-
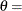 lower threshold parameter (lower endpoint parameter)
lower threshold parameter (lower endpoint parameter)
-
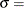 scale parameter
scale parameter 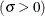
-
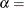 shape parameter
shape parameter 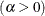
-
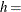 width of histogram interval
width of histogram interval
-
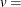 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
Note: This notation is consistent with that of other distributions that you can fit with the HISTOGRAM statement. However, many texts, including Johnson, Kotz, and Balakrishnan (1995), write the density function of power function distribution as
The two parameterizations are related as follows:
Note: The family of power function distributions is subclass of beta distribution with density function
where ![]() with parameter
with parameter ![]() . Therefore, all properties and estimation procedures of beta distribution apply.
. Therefore, all properties and estimation procedures of beta distribution apply.
The range of the power function distribution is bounded below by a threshold parameter ![]() and above by
and above by ![]() . If you specify a fitted power function curve by using the POWER option,
. If you specify a fitted power function curve by using the POWER option, ![]() must be less than the minimum data value and
must be less than the minimum data value and ![]() must be greater than the maximum data value. You can specify
must be greater than the maximum data value. You can specify ![]() and
and ![]() with the THETA= and SIGMA= power-options in parentheses after the keyword POWER. By default,
with the THETA= and SIGMA= power-options in parentheses after the keyword POWER. By default, ![]() and
and ![]() . If you specify THETA=EST and SIGMA=EST, maximum likelihood estimates are computed for
. If you specify THETA=EST and SIGMA=EST, maximum likelihood estimates are computed for ![]() and
and ![]() . However, three-parameter maximum likelihood estimation does not always converge.
. However, three-parameter maximum likelihood estimation does not always converge.
In addition, you can specify ![]() with the ALPHA= power-option. By default, the procedure calculates maximum likelihood estimate for
with the ALPHA= power-option. By default, the procedure calculates maximum likelihood estimate for ![]() . For example, to fit a power function density curve to a set of data bounded below by 32 and above by 212 with maximum likelihood
estimate for
. For example, to fit a power function density curve to a set of data bounded below by 32 and above by 212 with maximum likelihood
estimate for ![]() , use the following statement:
, use the following statement:
histogram Length / power(theta=32 sigma=180);
The fitted density function is
where
-
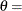 lower threshold parameter (lower endpoint parameter)
lower threshold parameter (lower endpoint parameter)
-
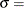 scale parameter
scale parameter 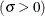
-
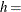 width of histogram interval
width of histogram interval
-
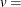 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
Note: The Rayleigh distribution is Weibull distribution with density function
and with shape parameter ![]() and scale parameter
and scale parameter ![]() .
.
The threshold parameter ![]() must be less than the minimum data value. You can specify
must be less than the minimum data value. You can specify ![]() with the THETA= Rayleigh-option. By default,
with the THETA= Rayleigh-option. By default, ![]() . In addition you can specify
. In addition you can specify ![]() with the SIGMA= Rayleigh-option. By default, the procedure calculates maximum likelihood estimate for
with the SIGMA= Rayleigh-option. By default, the procedure calculates maximum likelihood estimate for ![]() .
.
For example, to fit a Rayleigh density curve to a set of data bounded below by 32 with maximum likelihood estimate for ![]() , use the following statement:
, use the following statement:
histogram Length / rayleigh(theta=32);
The fitted density function is
![\[ p(x) = \left\{ \begin{array}{ll} \frac{\delta hv}{\sigma \sqrt {2\pi } } \left[ \left( \frac{x - \theta }{\sigma } \right) \left( 1 - \frac{x - \theta }{\sigma } \right) \right]^{-1} \times & \\ \exp \left[ -\frac{1}{2} \left( \gamma + \delta \log ( \frac{x - \theta }{\theta + \sigma -x} ) \right)^2 \right] & \mbox{for } \theta < x < \theta + \sigma \\ 0 & \mbox{for } x \leq \theta \text { or } x \geq \theta + \sigma \end{array} \right. \]](images/procstat_univariate0342.png)
where
-
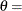 threshold parameter
threshold parameter 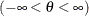
-
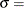 scale parameter
scale parameter 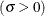
-
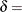 shape parameter
shape parameter 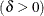
-
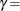 shape parameter
shape parameter 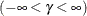
-
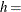 width of histogram interval
width of histogram interval
-
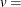 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
The ![]() distribution is bounded below by the parameter
distribution is bounded below by the parameter ![]() and above by the value
and above by the value ![]() . The parameter
. The parameter ![]() must be less than the minimum data value. You can specify
must be less than the minimum data value. You can specify ![]() with the THETA=
with the THETA= ![]() -option, or you can request that
-option, or you can request that ![]() be estimated with the THETA = EST
be estimated with the THETA = EST ![]() -option. The default value for
-option. The default value for ![]() is zero. The sum
is zero. The sum ![]() must be greater than the maximum data value. The default value for
must be greater than the maximum data value. The default value for ![]() is one. You can specify
is one. You can specify ![]() with the SIGMA=
with the SIGMA= ![]() -option, or you can request that
-option, or you can request that ![]() be estimated with the SIGMA = EST
be estimated with the SIGMA = EST ![]() -option.
-option.
By default, the method of percentiles given by Slifker and Shapiro (1980) is used to estimate the parameters. This method is based on four data percentiles, denoted by ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , which correspond to the four equally spaced percentiles of a standard normal distribution, denoted by
, which correspond to the four equally spaced percentiles of a standard normal distribution, denoted by ![]() ,
, ![]() , z, and
, z, and ![]() , under the transformation
, under the transformation
The default value of z is 0.524. The results of the fit are dependent on the choice of z, and you can specify other values with the FITINTERVAL= option (specified in parentheses after the SB option). If you use the method of percentiles, you should select a value of z that corresponds to percentiles which are critical to your application.
The following values are computed from the data percentiles:
It was demonstrated by Slifker and Shapiro (1980) that
![\[ \begin{array}{ll} \frac{mn}{p^2} > 1 & \mbox{for any }S_ U\text { distribution} \\ \frac{mn}{p^2} < 1 & \mbox{for any }S_ B\text { distribution} \\ \frac{mn}{p^2} = 1 & \mbox{for any }S_ L\text { (lognormal) distribution} \\ \end{array} \]](images/procstat_univariate0357.png)
A tolerance interval around one is used to discriminate among the three families with this ratio criterion. You can specify the tolerance with the FITTOLERANCE= option (specified in parentheses after the SB option). The default tolerance is 0.01. Assuming that the criterion satisfies the inequality
the parameters of the ![]() distribution are computed using the explicit formulas derived by Slifker and Shapiro (1980).
distribution are computed using the explicit formulas derived by Slifker and Shapiro (1980).
If you specify FITMETHOD = MOMENTS (in parentheses after the SB option), the method of moments is used to estimate the parameters. If you specify FITMETHOD = MLE (in parentheses after the SB option), the method of maximum likelihood is used to estimate the parameters. Note that maximum likelihood estimates may not always exist. Refer to Bowman and Shenton (1983) for discussion of methods for fitting Johnson distributions.
The fitted density function is
![\[ p(x) = \left\{ \begin{array}{ll} \frac{ \delta hv}{\sigma \sqrt {2\pi } } \frac{ 1 }{ \sqrt { 1 + \left( (x - \theta ) / \sigma \right)^2 } } \times & \\ \exp \left[ -\frac{1}{2} \left( \gamma + \delta \sinh ^{-1} \left( \frac{x - \theta }{\sigma } \right) \right)^2 \right] & \mbox{for } x > \theta \\ 0 & \mbox{for } x \leq \theta \end{array} \right. \]](images/procstat_univariate0359.png)
where
-
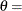 location parameter
location parameter 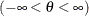
-
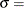 scale parameter
scale parameter 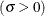
-
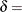 shape parameter
shape parameter 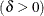
-
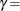 shape parameter
shape parameter 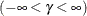
-
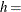 width of histogram interval
width of histogram interval
-
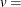 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
You can specify the parameters with the THETA=, SIGMA=, DELTA=, and GAMMA= ![]() -options, which are enclosed in parentheses after the SU option. If you do not specify these parameters, they are estimated.
-options, which are enclosed in parentheses after the SU option. If you do not specify these parameters, they are estimated.
By default, the method of percentiles given by Slifker and Shapiro (1980) is used to estimate the parameters. This method is based on four data percentiles, denoted by ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , which correspond to the four equally spaced percentiles of a standard normal distribution, denoted by
, which correspond to the four equally spaced percentiles of a standard normal distribution, denoted by ![]() ,
, ![]() , z, and
, z, and ![]() , under the transformation
, under the transformation
The default value of z is 0.524. The results of the fit are dependent on the choice of z, and you can specify other values with the FITINTERVAL= option (specified in parentheses after the SU option). If you use the method of percentiles, you should select a value of z that corresponds to percentiles that are critical to your application.
The following values are computed from the data percentiles:
It was demonstrated by Slifker and Shapiro (1980) that
![\[ \begin{array}{ll} \frac{mn}{p^2} > 1 & \mbox{for any }S_ U\text { distribution} \\ \frac{mn}{p^2} < 1 & \mbox{for any }S_ B\text { distribution} \\ \frac{mn}{p^2} = 1 & \mbox{for any }S_ L\text { (lognormal) distribution} \\ \end{array} \]](images/procstat_univariate0357.png)
A tolerance interval around one is used to discriminate among the three families with this ratio criterion. You can specify the tolerance with the FITTOLERANCE= option (specified in parentheses after the SU option). The default tolerance is 0.01. Assuming that the criterion satisfies the inequality
the parameters of the ![]() distribution are computed using the explicit formulas derived by Slifker and Shapiro (1980).
distribution are computed using the explicit formulas derived by Slifker and Shapiro (1980).
If you specify FITMETHOD = MOMENTS (in parentheses after the SU option), the method of moments is used to estimate the parameters. If you specify FITMETHOD = MLE (in parentheses after the SU option), the method of maximum likelihood is used to estimate the parameters. Note that maximum likelihood estimates do not always exist. Refer to Bowman and Shenton (1983) for discussion of methods for fitting Johnson distributions.
The fitted density function is
where
-
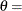 threshold parameter
threshold parameter
-
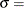 scale parameter
scale parameter 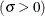
-
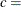 shape parameter
shape parameter 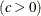
-
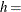 width of histogram interval
width of histogram interval
-
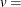 vertical scaling factor
vertical scaling factor
and
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
The threshold parameter ![]() must be less than the minimum data value. You can specify
must be less than the minimum data value. You can specify ![]() with the THRESHOLD= Weibull-option. By default,
with the THRESHOLD= Weibull-option. By default, ![]() . If you specify THETA=EST, a maximum likelihood estimate is computed for
. If you specify THETA=EST, a maximum likelihood estimate is computed for ![]() . You can specify
. You can specify ![]() and c with the SCALE= and SHAPE= Weibull-options, respectively. By default, the procedure calculates maximum likelihood estimates for
and c with the SCALE= and SHAPE= Weibull-options, respectively. By default, the procedure calculates maximum likelihood estimates for ![]() and c.
and c.
The exponential distribution is a special case of the Weibull distribution where ![]() .
.
You can use the DATA step function QUANTILE to compute Weibull quantiles and the DATA step function CDF to compute Weibull probabilities.