The CORR Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Pearson Product-Moment CorrelationSpearman Rank-Order CorrelationKendall’s Tau-b Correlation CoefficientHoeffding Dependence CoefficientPartial CorrelationFisher’s z TransformationPolychoric CorrelationPolyserial CorrelationCronbach’s Coefficient AlphaConfidence and Prediction EllipsesMissing ValuesIn-Database ComputationOutput TablesOutput Data SetsODS Table NamesODS Graphics
Pearson Product-Moment CorrelationSpearman Rank-Order CorrelationKendall’s Tau-b Correlation CoefficientHoeffding Dependence CoefficientPartial CorrelationFisher’s z TransformationPolychoric CorrelationPolyserial CorrelationCronbach’s Coefficient AlphaConfidence and Prediction EllipsesMissing ValuesIn-Database ComputationOutput TablesOutput Data SetsODS Table NamesODS Graphics -
Examples
 Computing Four Measures of AssociationComputing Correlations between Two Sets of VariablesAnalysis Using Fisher’s z TransformationApplications of Fisher’s z TransformationComputing Polyserial CorrelationsComputing Cronbach’s Coefficient AlphaSaving Correlations in an Output Data SetCreating Scatter PlotsComputing Partial Correlations
Computing Four Measures of AssociationComputing Correlations between Two Sets of VariablesAnalysis Using Fisher’s z TransformationApplications of Fisher’s z TransformationComputing Polyserial CorrelationsComputing Cronbach’s Coefficient AlphaSaving Correlations in an Output Data SetCreating Scatter PlotsComputing Partial Correlations - References
Pearson Product-Moment Correlation
The Pearson product-moment correlation is a parametric measure of association for two variables. It measures both the strength
and the direction of a linear relationship. If one variable X is an exact linear function of another variable Y, a positive relationship exists if the correlation is 1 and a negative relationship exists if the correlation is ![]() 1. If there is no linear predictability between the two variables, the correlation is 0. If the two variables are normal with
a correlation 0, the two variables are independent. However, correlation does not imply causality because, in some cases,
an underlying causal relationship might not exist.
1. If there is no linear predictability between the two variables, the correlation is 0. If the two variables are normal with
a correlation 0, the two variables are independent. However, correlation does not imply causality because, in some cases,
an underlying causal relationship might not exist.
The scatter plot matrix in Figure 2.4 displays the relationship between two numeric random variables in various situations.
Figure 2.4: Correlations between Two Variables
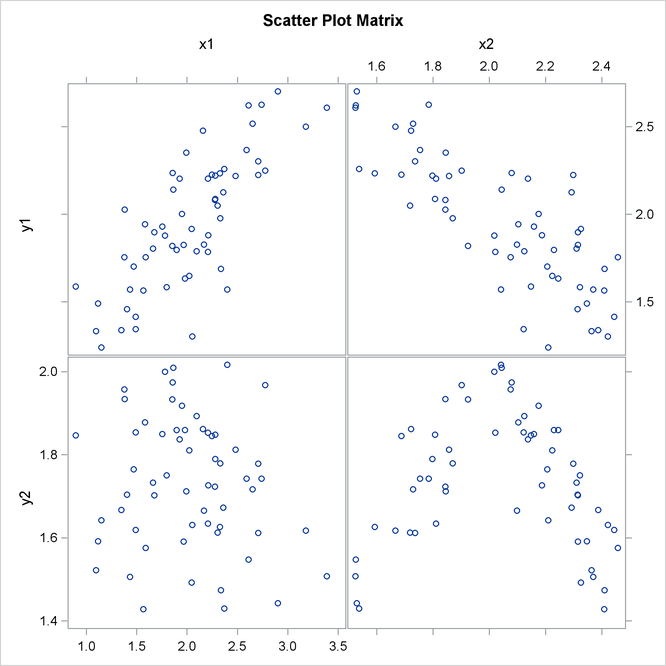
The scatter plot matrix shows a positive correlation between variables Y1 and X1, a negative correlation between Y1 and X2, and no clear correlation between Y2 and X1. The plot also shows no clear linear correlation between Y2 and X2, even though Y2 is dependent on X2.
The formula for the population Pearson product-moment correlation, denoted ![]() , is
, is
|
|
The sample correlation, such as a Pearson product-moment correlation or weighted product-moment correlation, estimates the population correlation. The formula for the sample Pearson product-moment correlation is
|
|
where ![]() is the sample mean of
is the sample mean of ![]() and
and ![]() is the sample mean of
is the sample mean of ![]() . The formula for a weighted Pearson product-moment correlation is
. The formula for a weighted Pearson product-moment correlation is
|
|
where ![]() is the weight,
is the weight, ![]() is the weighted mean of
is the weighted mean of ![]() , and
, and ![]() is the weighted mean of
is the weighted mean of ![]() .
.