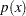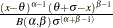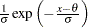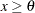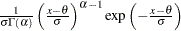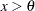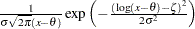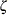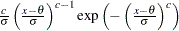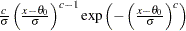Beta Distribution

To create the plot, the observations are ordered from smallest to largest, and the th ordered observation is plotted against the quantile 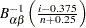, where 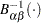is the inverse normalized incomplete beta function, is the number of nonmissing observations, and and 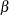are the shape parameters of the beta distribution. In a probability plot, the horizontal axis is scaled in percentile units.

The pattern on the plot for ALPHA= and BETA=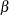 tends to be linear with intercept 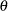and slope if the data are beta distributed with the specific density function

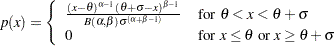where 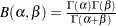and

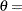lower threshold parameter

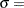scale parameter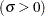

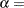first shape parameter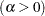

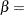second shape parameter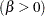

Exponential Distribution

To create the plot, the observations are ordered from smallest to largest, and the 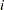th ordered observation is plotted against the quantile 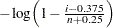, where is the number of nonmissing observations. In a probability plot, the horizontal axis is scaled in percentile units.

The pattern on the plot tends to be linear with intercept 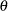and slope if the data are exponentially distributed with the specific density function

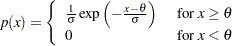where 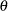is a threshold parameter, and is a positive scale parameter.

Gamma Distribution

To create the plot, the observations are ordered from smallest to largest, and the 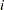th ordered observation is plotted against the quantile 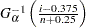, where 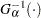is the inverse normalized incomplete gamma function, is the number of nonmissing observations, and is the shape parameter of the gamma distribution. In a probability plot, the horizontal axis is scaled in percentile units.

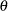The pattern on the plot for ALPHA= tends to be linear with intercept and slope if the data are gamma distributed with the specific density function

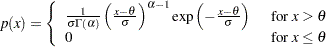where

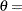threshold parameter

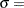scale parameter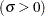

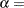shape parameter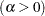

Lognormal Distribution

To create the plot, the observations are ordered from smallest to largest, and the 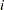th ordered observation is plotted against the quantile 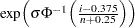, where is the inverse cumulative standard normal distribution, is the number of nonmissing observations, and is the shape parameter of the lognormal distribution. In a probability plot, the horizontal axis is scaled in percentile units.

The pattern on the plot for SIGMA= tends to be linear with intercept 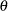and slope 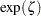if the data are lognormally distributed with the specific density function

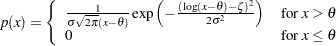where

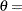threshold parameter

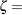scale parameter

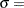shape parameter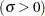

See Example 4.26 and Example 4.33.

Normal Distribution

To create the plot, the observations are ordered from smallest to largest, and the 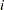th ordered observation is plotted against the quantile 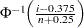, where is the inverse cumulative standard normal distribution and is the number of nonmissing observations. In a probability plot, the horizontal axis is scaled in percentile units.

The point pattern on the plot tends to be linear with intercept 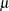and slope if the data are normally distributed with the specific density function

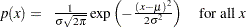where 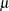is the mean and is the standard deviation ().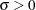

Three-Parameter Weibull Distribution

To create the plot, the observations are ordered from smallest to largest, and the 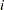th ordered observation is plotted against the quantile , where is the number of nonmissing observations, and is the Weibull distribution shape parameter. In a probability plot, the horizontal axis is scaled in percentile units.

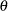The pattern on the plot for C= tends to be linear with intercept and slope if the data are Weibull distributed with the specific density function

where

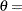threshold parameter

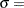scale parameter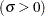

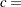shape parameter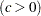

See Example 4.34.

Two-Parameter Weibull Distribution

To create the plot, the observations are ordered from smallest to largest, and the log of the shifted 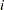th ordered observation 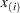, denoted by 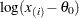, is plotted against the quantile 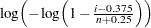, where is the number of nonmissing observations. In a probability plot, the horizontal axis is scaled in percentile units.

Unlike the three-parameter Weibull quantile, the preceding expression is free of distribution parameters. Consequently, the C= shape parameter is not mandatory with the WEIBULL2 distribution option.

The pattern on the plot for THETA=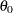 tends to be linear with intercept 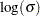and slope 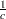if the data are Weibull distributed with the specific density function

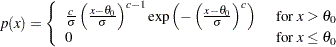where

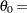known lower threshold

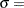scale parameter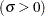

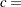shape parameter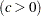

See Example 4.34.