The HPIMPUTE Procedure
PROC HPIMPUTE first computes the imputation value and then imputes with that value. Some statistics (such as the mean, minimum, and maximum) are computed precisely. The pseudomedian, which is calculated if you specify METHOD=PMEDIAN in the IMPUTE statement, is an estimation of the median. The computation of the median requires sorting the entire data. However, in a distributed computing environment, each grid node contains only a part of the entire data. Sorting all the data in such an environment requires a lot of internode communications, degrading the performance dramatically. To address this challenge, a binning-based method is used to estimate the pseudomedian.
For variable x, assume that the data set is {![]() }, where
}, where ![]() . Let
. Let ![]() , and let
, and let ![]() . The range of the variable is
. The range of the variable is ![]() .
.
A simple bucket binning method is used to obtain the basic information. Let ![]() be the number of buckets, ranging from
be the number of buckets, ranging from ![]() to
to ![]() . For each bucket
. For each bucket ![]() ,
, ![]() , PROC HPIMPUTE keeps following information:
, PROC HPIMPUTE keeps following information:
-
 : count of
: count of  in
in 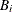
-
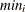 : minimum value of
: minimum value of  in
in 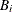
-
 : maximum value of
: maximum value of  in
in 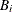
For each bucket ![]() , the range
, the range ![]() is
is
where ![]()
To calculate the pseudomedian, PROC HPIMPUTE finds the smallest ![]() , such that
, such that ![]() , where
, where ![]() is the number of nonmissing observations of
is the number of nonmissing observations of ![]() in the data set. Therefore, the pseudomedian value
in the data set. Therefore, the pseudomedian value ![]() is
is
![]() is set to 10,000 in PROC HPIMPUTE. Experiments show that the pseudomedian is a good estimate of the median and that the performance
is satisfactory.
is set to 10,000 in PROC HPIMPUTE. Experiments show that the pseudomedian is a good estimate of the median and that the performance
is satisfactory.
