| The DTREE Procedure |
Example 7.5 Loan Grant Decision Problem
Many financial decisions are difficult to analyze because of the variety of available strategies and the continuous nature of the problem. However, if the alternatives and time frame can be restricted, then decision analysis can be a useful analysis tool.
For example, a loan officer is faced with the problem of deciding whether to approve or deny an application for a one-year $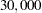 loan at the current rate of
loan at the current rate of 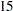 % of interest. If the application is approved, the borrower will either pay off the loan in full after one year or default. Based on experience, the default rate is about
% of interest. If the application is approved, the borrower will either pay off the loan in full after one year or default. Based on experience, the default rate is about 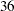 out of
out of 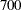 . If the loan is denied, the money is put in government bonds at the interest rate of
. If the loan is denied, the money is put in government bonds at the interest rate of 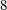 %.
%.
To obtain more information about the applicant, the loan officer engages a credit investigation unit at a cost of $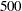 per person that will give either a positive recommendation for making a loan or a negative recommendation. Past experience with this investigator yields that of those who ultimately paid off their loans,
per person that will give either a positive recommendation for making a loan or a negative recommendation. Past experience with this investigator yields that of those who ultimately paid off their loans, 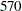 out of
out of 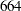 were given a positive recommendation. On the other hand,
were given a positive recommendation. On the other hand, 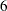 out of
out of 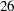 that had defaulted had also been given a positive recommendation by the investigator.
that had defaulted had also been given a positive recommendation by the investigator.
The STAGEIN= data set, Stage6, gives the structure of the decision problem.
/* -- create the STAGEIN= data set -- */ data Stage6; format _STNAME_ $14. _STTYPE_ $2. _OUTCOM_ $20. _SUCC_ $14. ; input _STNAME_ $ _STTYPE_ $ _OUTCOM_ & _SUCC_ $ ; datalines; Application D Approve loan Payment . . Deny loan . Payment C Pay off . . . Default . Investigation D Order investigation Recommendation . . Do not order Application Recommendation C Positive Application . . Negative Application ;
The PROBIN= data set Prob6 gives the probability distributions for the random events at the chance nodes.
/* -- create the PROBIN= data set -- */ data Prob6; length _GIVEN_ _EVENT1_ _EVENT2_ $16; _EVENT1_='Pay off'; _EVENT2_='Default'; _PROB1_=664/700; _PROB2_=1.0-_PROB1_; output; _GIVEN_='Pay off'; _EVENT1_='Positive'; _EVENT2_='Negative'; _PROB1_=570/664; _PROB2_=1.0-_PROB1_; output; _GIVEN_='Default'; _EVENT1_='Positive'; _EVENT2_='Negative'; _PROB1_=6/26; _PROB2_=1.0-_PROB1_; output; run;
The PAYOFFS= data set Payoff6 gives the payoffs for the various scenarios. Notice that the first observation in this data set indicates that if the officer denies the loan application, then payoffs are the interest from the money invested in government bonds. The second and the third observations are redundant for the basic analysis but are needed to determine the value of information as shown later.
/* -- create the PAYOFFS= data set -- */ data Payoff6(drop=loan); length _STATE_ _ACT_ $24; loan=30000; _ACT_='Deny loan'; _VALUE_=loan*0.08; output; _STATE_='Pay off'; _VALUE_=loan*0.08; output; _STATE_='Default'; _VALUE_=loan*0.08; output; _ACT_='Approve loan'; _STATE_='Pay off'; _VALUE_=loan*0.15; output; _STATE_='Default'; _VALUE_=-1.0*loan; output; run;
The following code invokes the DTREE procedure to solve this decision problem.
/* -- define title -- */
title 'Loan Grant Decision';
/* -- PROC DTREE statements -- */
proc dtree
stagein=Stage6 probin=Prob6 payoffs=Payoff6
summary target=investigation nowarning;
modify 'Order investigation' reward -500;
evaluate;
OPTIONS LINESIZE=85;
summary / target=Application;
OPTIONS LINESIZE=80;
Note that the $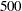 investigation fee is not included in the Stage6 data set. Since the outcome 'Order investigation' is the only outcome that has a nonzero reward, it is easier to set the reward for this outcome using the MODIFY statement. The quotes that enclose the outcome name in the MODIFY statement are necessary because the outcome name contains a space.
investigation fee is not included in the Stage6 data set. Since the outcome 'Order investigation' is the only outcome that has a nonzero reward, it is easier to set the reward for this outcome using the MODIFY statement. The quotes that enclose the outcome name in the MODIFY statement are necessary because the outcome name contains a space.
The results in Output 7.5.1 and Output 7.5.2 indicate that it is optimal to do the following:
The loan officer should order the credit investigation and approve the loan application if the investigator gives the applicant a positive recommendation. On the other hand, he should deny the application if a negative recommendation is given to the applicant.
Furthermore, the loan officer should order a credit investigation if the cost for the investigation is less than
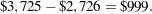
| Order of Stages | |
|---|---|
| Stage | Type |
| Investigation | Decision |
| Recommendation | Chance |
| Application | Decision |
| Payment | Chance |
| _ENDST_ | End |
| Order of Stages | |
|---|---|
| Stage | Type |
| Investigation | Decision |
| Recommendation | Chance |
| Application | Decision |
| Payment | Chance |
| _ENDST_ | End |
| Decision Parameters | |
|---|---|
| Decision Criterion: | Maximize Expected Value (MAXEV) |
| Optimal Decision Yields: | 3225 |
| Optimal Decision Policy | ||||
|---|---|---|---|---|
| Up to Stage Application | ||||
| Alternatives or Outcomes | Cumulative Reward |
Evaluating Value | ||
| Order investigation | Positive | Approve loan | -500 | 4004* |
| Order investigation | Positive | Deny loan | -500 | 2400 |
| Order investigation | Negative | Approve loan | -500 | -3351 |
| Order investigation | Negative | Deny loan | -500 | 2400* |
| Do not order | Approve loan | 0 | 2726* | |
| Do not order | Deny loan | 0 | 2400 | |
Now, the loan officer learns of another credit investigation company that claims to have a more accurate credit checking system for predicting whether the applicants will default on their loans. However, he has not been able to find out what the company charges for their service or how accurate their credit checking system is. Perhaps the best thing he can do at this stage is to assume that the company can predict perfectly whether or not applicants will default on their loans and determine the maximum amount to pay for this perfect investigation. The answer to this question can be found with the PROC DTREE statements:
save;
move payment before investigation;
evaluate;
recall;
Notice that moving the stage 'Payment' to the beginning of the tree means that the new decision tree contains two scenarios that are not in the original tree: the scenario 'Pay off' and 'Deny loan', and the scenario 'Default' and 'Deny loan'. The second and third observations in the Payoff6 data set supply values for these new scenarios. If these records are not included in the PAYOFFS= data set, then PROC DTREE assumes they are  .
.
Also notice that the SUMMARY and TARGET= options are specified globally in the PROC DTREE statement and hence are not needed in the EVALUATE statement. The results from the DTREE procedure are displayed in Output 7.5.3.
| Order of Stages | |
|---|---|
| Stage | Type |
| Payment | Chance |
| Investigation | Decision |
| Recommendation | Chance |
| Application | Decision |
| _ENDST_ | End |
| Decision Parameters | |
|---|---|
| Decision Criterion: | Maximize Expected Value (MAXEV) |
| Optimal Decision Yields: | 4392 |
| Optimal Decision Policy | |||
|---|---|---|---|
| Up to Stage Investigation | |||
| Alternatives or Outcomes | Cumulative Reward |
Evaluating Value | |
| Pay off | Order investigation | -500 | 4500 |
| Pay off | Do not order | 0 | 4500* |
| Default | Order investigation | -500 | 2400 |
| Default | Do not order | 0 | 2400* |
The optimal decision summary in Output 7.5.3 shows that the yields with perfect investigation is $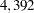 . Recall that the yield of alternative 'Do not order' the investigation, as shown in Output 7.5.1, is $
. Recall that the yield of alternative 'Do not order' the investigation, as shown in Output 7.5.1, is $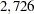 . Therefore, the maximum amount he should pay for the perfect investigation can be determined easily as
. Therefore, the maximum amount he should pay for the perfect investigation can be determined easily as
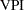 |
 |
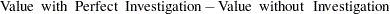 |
|||
 |
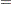 |
 |
|||
 |
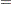 |
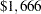 |
Note that if you use the VPI statement to determine the value of a perfect investigation, the result is different from the value calculated previously.
vpi payment;
NOTE: The currently optimal decision yields 3225.4725275.
NOTE: The new optimal decision yields 4392.
NOTE: The value of perfect information of stage Payment
yields 1166.5274725.
The reason for this difference is that the VPI statement causes PROC DTREE first to determine the value with perfect information, then to compare this value with the value with current information available (in this example, it is the recommendation from the original investigation unit). Therefore, the VPI statement returns a value that is calculated as
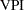 |
 |
 |
|||
 |
 |
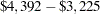 |
|||
 |
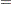 |
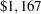 |
The loan officer considered another question regarding the maximum amount he should pay to a company to help collect the principal and the interest if an applicant defaults on the loan. This question is similar to the question concerning the improvement that can be expected if he can control whether or not an applicant will default on his loan (of course he will always want the applicant to pay off in full after one year). The answer to this question can be obtained with the following statements:
modify payment type;
evaluate;
| Order of Stages | |
|---|---|
| Stage | Type |
| Investigation | Decision |
| Recommendation | Chance |
| Application | Decision |
| Payment | Decision |
| _ENDST_ | End |
| Decision Parameters | |
|---|---|
| Decision Criterion: | Maximize Expected Value (MAXEV) |
| Optimal Decision Yields: | 4500 |
| Optimal Decision Policy | ||
|---|---|---|
| Up to Stage Investigation | ||
| Alternatives or Outcomes | Cumulative Reward |
Evaluating Value |
| Order investigation | -500 | 4500 |
| Do not order | 0 | 4500* |
The result is obvious and is shown in Output 7.5.4. Using a calculation similar to the one used to calculate the value of a perfect investigation, the maximum amount one should pay for this kind of service is 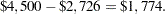 As previously described, this value is different from the value obtained by using the VPC statement. In fact, if you specify the statement
As previously described, this value is different from the value obtained by using the VPC statement. In fact, if you specify the statement
vpc payment;
you get the value of VPC, which is $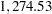 , from the SAS log as
, from the SAS log as
NOTE: The currently optimal decision yields 3225.4725275.
NOTE: The new optimal decision yields 4500.
NOTE: The value of perfect control of stage Payment yields
1274.5274725.
Obviously, all of the values of investigation and other services depend on the value of the loan. Since each of the payoffs for the various scenarios given in the Payoff6 data set is proportional to the value of loan, you can safely assume that the value of the loan is 1 unit and determine the ratio of the value for a particular service to the value of the loan. To obtain these ratios, change the value of the variable LOAN to  in the Payoff6 data set and invoke PROC DTREE again as follows:
in the Payoff6 data set and invoke PROC DTREE again as follows:
/* -- create the alternative PAYOFFS= data set -- */
data Payoff6a(drop=loan);
length _STATE_ _ACT_ $24;
loan=1;
_ACT_='Deny loan'; _VALUE_=loan*0.08; output;
_STATE_='Pay off'; _VALUE_=loan*0.08; output;
_STATE_='Default'; _VALUE_=loan*0.08; output;
_ACT_='Approve loan';
_STATE_='Pay off'; _VALUE_=loan*0.15; output;
_STATE_='Default'; _VALUE_=-1.0*loan; output;
run;
/* -- PROC DTREE statements -- */
title 'Loan Grant Decision';
proc dtree
stagein=Stage6 probin=Prob6 payoffs=Payoff6a
nowarning;
evaluate / summary target=investigation;
save;
move payment before investigation;
evaluate;
recall;
modify payment type;
evaluate;
quit;
The optimal decision summary given in Output 7.5.5 shows that the ratio of the value of investigation that the loan officer currently engages in to the value of the loan is 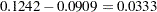 to
to  .
.
 Unit Loan
Unit Loan
| Order of Stages | |
|---|---|
| Stage | Type |
| Investigation | Decision |
| Recommendation | Chance |
| Application | Decision |
| Payment | Chance |
| _ENDST_ | End |
| Decision Parameters | |
|---|---|
| Decision Criterion: | Maximize Expected Value (MAXEV) |
| Optimal Decision Yields: | 0.1242 |
| Optimal Decision Policy | ||
|---|---|---|
| Up to Stage Investigation | ||
| Alternatives or Outcomes | Cumulative Reward | Evaluating Value |
| Order investigation | 0.1242* | |
| Do not order | 0.0909 | |
The following messages are written to the SAS log:
NOTE: Present order of stages:
Investigation(D), Recommendation(C), Application(D),
Payment(C), _ENDST_(E).
NOTE: The current problem has been successfully saved.
NOTE: Present order of stages:
Payment(C), Investigation(D), Recommendation(C),
Application(D), _ENDST_(E).
NOTE: The currently optimal decision yields 0.1464.
NOTE: The original problem has been successfully recalled.
NOTE: Present order of stages:
Investigation(D), Recommendation(C), Application(D),
Payment(C), _ENDST_(E).
NOTE: The type of stage Payment has been changed.
NOTE: The currently optimal decision yields 0.15.
The preceding messages show that the ratio of the value of perfect investigation to the value of a loan is 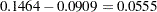 to
to  , and the ratio of the maximum amount the officer should pay for perfect control to the value of loan is
, and the ratio of the maximum amount the officer should pay for perfect control to the value of loan is  to 1.
to 1.
Output 7.5.6, produced by the following statements, shows a table of the values of the investigation currently engaged in, the values of perfect investigation, and the values of perfect control for loans ranging from $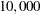 to $
to $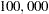 .
.
/* create the data set for value of loan */
/* and corresponding values of services */
data Datav6(drop=k ratio1 ratio2 ratio3);
label loan="Value of Loan"
vci="Value of Current Credit Investigation"
vpi="Value of Perfect Credit Investigation"
vpc="Value of Perfect Collecting Service";
/* calculate ratios */
ratio1=0.1242-0.0909;
ratio2=0.1464-0.0909;
ratio3=0.15-0.0909;
Loan=0;
do k=1 to 10;
/* set the value of loan */
loan=loan+10000;
/* calculate the values of various services */
vci=loan*ratio1;
vpi=loan*ratio2;
vpc=loan*ratio3;
/* output current observation */
output;
end;
run;
/* print the table of the value of loan */
/* and corresponding values of services */
title 'Value of Services by Value of Loan';
proc print label;
format loan vci vpi vpc dollar12.0;
run;
| Value of Services by Value of Loan |
| Obs | Value of Loan | Value of Current Credit Investigation |
Value of Perfect Credit Investigation |
Value of Perfect Collecting Service |
|---|---|---|---|---|
| 1 | $10,000 | $333 | $555 | $591 |
| 2 | $20,000 | $666 | $1,110 | $1,182 |
| 3 | $30,000 | $999 | $1,665 | $1,773 |
| 4 | $40,000 | $1,332 | $2,220 | $2,364 |
| 5 | $50,000 | $1,665 | $2,775 | $2,955 |
| 6 | $60,000 | $1,998 | $3,330 | $3,546 |
| 7 | $70,000 | $2,331 | $3,885 | $4,137 |
| 8 | $80,000 | $2,664 | $4,440 | $4,728 |
| 9 | $90,000 | $2,997 | $4,995 | $5,319 |
| 10 | $100,000 | $3,330 | $5,550 | $5,910 |
Copyright © SAS Institute, Inc. All Rights Reserved.