The OPTNET Procedure

Transitive Closure

Subsections:

The transitive closure of a graph $G$ is a graph $G^ T = (N,A^ T)$ such that for all $i,j \in N$ there is a link $(i,j) \in A^ T$ if and only if there exists a path from i to j in $G$.

The transitive closure of a graph can help to efficiently answer questions about reachability. Suppose you want to answer the question of whether you can get from node i to node j in the original graph $G$. Given the transitive closure $G^ T$ of $G$, you can simply check for the existence of link $(i,j)$ to answer the question. Transitive closure has many applications, including speeding up the processing of structured query languages, which are often used in databases.

In PROC OPTNET, you can invoke the transitive closure algorithm by using the TRANSITIVE_CLOSURE statement. The options for this statement are described in the section TRANSITIVE_CLOSURE Statement.

The results for the transitive closure algorithm are written to the output data set that is specified in the OUT= option in the TRANSITIVE_CLOSURE statement. The links that define the transitive closure are listed in the output data set with variable names from and to.

The transitive closure algorithm reports status information in a macro variable called _OROPTNET_TRANSCL_. See the section Macro Variable _OROPTNET_TRANSCL_ for more information about this macro variable.

The algorithm that the PROC OPTNET uses to compute transitive closure is a sparse version of the Floyd-Warshall algorithm (Cormen, Leiserson, and Rivest 1990). This algorithm runs in time $O(|N|^3)$ and therefore might not scale to very large graphs.

Transitive Closure of a Simple Directed Graph

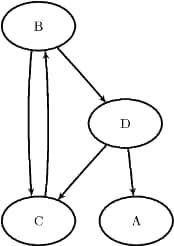
This example illustrates the use of the transitive closure algorithm on the simple directed graph $G$, which is shown in Figure 2.59.

Figure 2.59: A Simple Directed Graph $G$

A Simple Directed Graph G


The directed graph $G$ can be represented by the following links data set LinkSetIn: 

data LinkSetIn;
   input from $ to $ @@;
   datalines;
B C  B D  C B  D A  D C
;

The following statements calculate the transitive closure and output the results in the data set TransClosure: 

proc optnet
   graph_direction = directed
   data_links      = LinkSetIn;
   transitive_closure
      out          = TransClosure;
run;

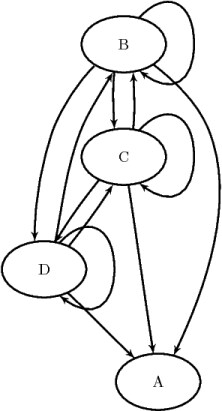
The data set TransClosure contains the transitive closure of $G$ and is shown in Figure 2.60.

Figure 2.60: Transitive Closure of a Simple Directed Graph

Transitive Closure

from to
B C
B D
C B
D A
D C
C C
C D
B B
D B
D D
B A
C A 




               

               


               
The transitive closure of $G$ is shown graphically in Figure 2.61. 
               

               
  

               


Figure 2.61: Transitive Closure of $G$

                  

                     
Transitive Closure of G

                  

               

               


               
For a more detailed example, see Transitive Closure for Identification of Circular Dependencies in a Bug Tracking System.