The OPTNET Procedure

A path in a graph is a sequence of nodes, each of which has a link to the next node in the sequence. A cycle is a path in which the start node and end node are the same.

In PROC OPTNET, you can find the cycles (or just count the cycles) of an input graph by invoking the CYCLE statement. The options for this statement are described in the section CYCLE Statement. To find the cycles and report them in an output data set, use the OUT= option. To simply count the cycles, do not use the OUT= option.

For undirected graphs, each link represents two directed links. For this reason, the following cycles are filtered out: trivial cycles () and duplicate cycles that are found by traversing a cycle in both directions ( and ).

The results for the cycle detection algorithm are written to the output data set that is specified in the OUT= option in the CYCLE statement. Each node of each cycle is listed in the OUT= data set along with the variable cycle to identify the cycle to which it belongs. The variable order defines the order (sequence) of the node in the cycle.

The cycle detection algorithm reports status information in a macro variable called _OROPTNET_CYCLE_. See the section Macro Variable _OROPTNET_CYCLE_ for more information about this macro variable.

The algorithm that PROC OPTNET uses to compute all cycles is a variant of the algorithm found in Johnson 1975. This algorithm runs in time , where c is the number of elementary cycles in the graph. So, the algorithm should scale to large graphs that contain few cycles. However, some graphs can have a very large number of cycles, so the algorithm might not scale.

If MODE=ALL_CYCLES and there are many cycles, the OUT= data set can become very large. It might be beneficial to check the number of cycles before you try to create the OUT= data set. When you specify MODE=FIRST_CYCLE, the algorithm returns the first cycle it finds and stops processing. This should run relatively quickly. On large-scale graphs, the MINLINKWEIGHT= and MAXLINKWEIGHT= options can be relatively expensive and might increase the computation time. See the section CYCLE Statement for more information about these options.

Cycle Detection of a Simple Directed Graph

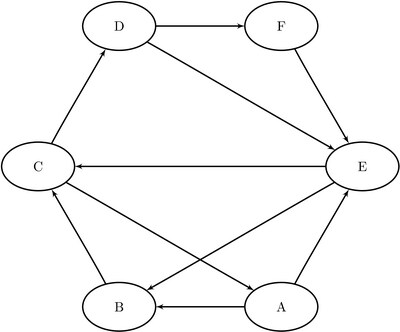
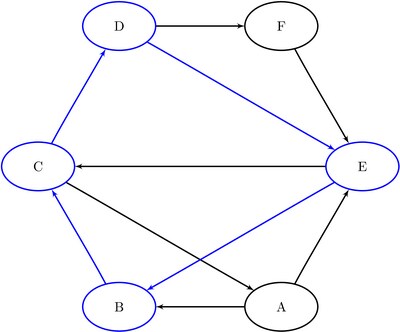
This section provides a simple example for using the cycle detection algorithm on the simple directed graph that is shown in Figure 2.26. Two other examples are Cycle Detection for Kidney Donor Exchange, which shows the use of cycle detection for optimizing a kidney donor exchange, and Transitive Closure for Identification of Circular Dependencies in a Bug Tracking System, which shows another application of cycle detection.

Figure 2.26: A Simple Directed Graph

The directed graph can be represented by the following links data set LinkSetIn:

data LinkSetIn;
   input from $ to $ @@;
   datalines;
A B  A E  B C  C A  C D
D E  D F  E B  E C  F E
;

The following statements check whether the graph has a cycle:

proc optnet
   graph_direction = directed
   data_links      = LinkSetIn;
   cycle
      mode         = first_cycle;
run;
%put &_OROPTNET_;
%put &_OROPTNET_CYCLE_;

The result is written to the log of the procedure, as shown Figure 2.27.

Figure 2.27: PROC OPTNET Log: Check the Existence of a Cycle in a Simple Directed Graph

NOTE: ------------------------------------------------------------------------------------------

NOTE: Running OPTNET version 13.2.

NOTE: ------------------------------------------------------------------------------------------

NOTE: Data input used 0.00 (cpu: 0.00) seconds.

NOTE: The number of nodes in the input graph is 6.

NOTE: The number of links in the input graph is 10.

NOTE: ------------------------------------------------------------------------------------------

NOTE: Processing cycle detection.

NOTE: The graph does have a cycle.

NOTE: Processing cycle detection used 0.00 (cpu: 0.00) seconds.

NOTE: ------------------------------------------------------------------------------------------

NOTE: Data output used 0.00 (cpu: 0.00) seconds.

NOTE: ------------------------------------------------------------------------------------------

STATUS=OK  CYCLE=OK

STATUS=OK  NUM_CYCLES=1  CPU_TIME=0.00  REAL_TIME=0.00

The following statements count the number of cycles in the graph:

proc optnet
   graph_direction = directed
   data_links      = LinkSetIn;
   cycle
      mode         = all_cycles;
run;
%put &_OROPTNET_;
%put &_OROPTNET_CYCLE_;

The result is written to the log of the procedure, as shown in Figure 2.28.

Figure 2.28: PROC OPTNET Log: Count the Number of Cycles in a Simple Directed Graph

NOTE: ------------------------------------------------------------------------------------------

NOTE: Running OPTNET version 13.2.

NOTE: ------------------------------------------------------------------------------------------

NOTE: Data input used 0.00 (cpu: 0.00) seconds.

NOTE: The number of nodes in the input graph is 6.

NOTE: The number of links in the input graph is 10.

NOTE: ------------------------------------------------------------------------------------------

NOTE: Processing cycle detection.

NOTE: The graph has 7 cycles.

NOTE: Processing cycle detection used 0.00 (cpu: 0.00) seconds.

NOTE: ------------------------------------------------------------------------------------------

NOTE: Data output used 0.00 (cpu: 0.00) seconds.

NOTE: ------------------------------------------------------------------------------------------

STATUS=OK  CYCLE=OK

STATUS=OK  NUM_CYCLES=7  CPU_TIME=0.00  REAL_TIME=0.00

The following statements return the first cycle found in the graph:

proc optnet
   graph_direction = directed
   data_links      = LinkSetIn;
   cycle
      out          = Cycles
      mode         = first_cycle;
run;

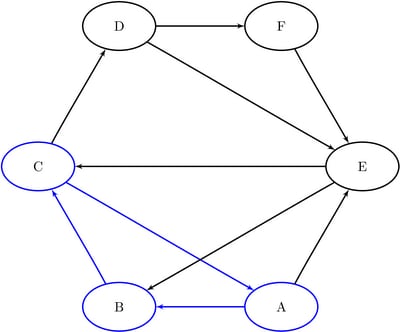
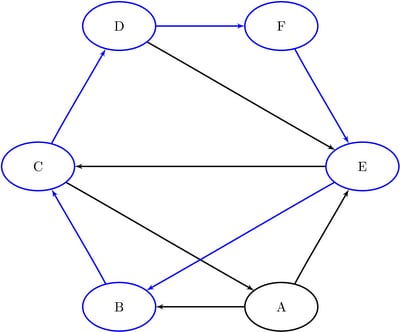
The data set Cycles now contains the first cycle found in the input graph; it is shown in Figure 2.29.

Figure 2.29: First Cycle Found in a Simple Directed Graph

cycle	order	node
1	1	A
1	2	B
1	3	C
1	4	A

The first cycle found in the input graph is shown graphically in Figure 2.30.

Figure 2.30:

The following statements return all of the cycles in the graph:

proc optnet
   graph_direction = directed
   data_links      = LinkSetIn;
   cycle
      out          = Cycles
      mode         = all_cycles;
run;

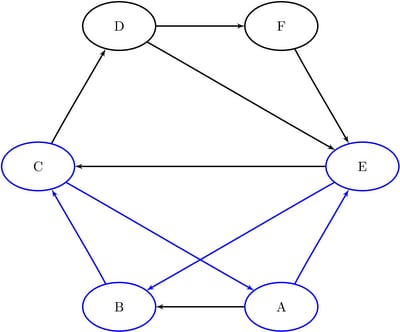
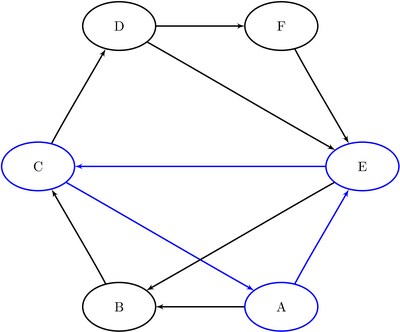
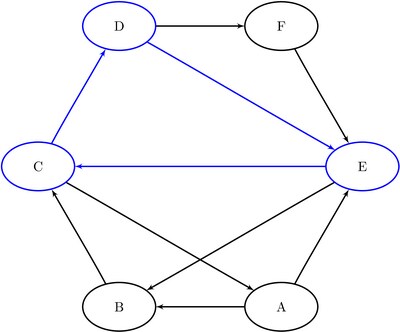
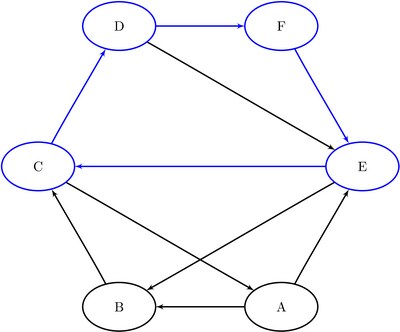
The data set Cycles now contains all of the cycles in the input graph; it is shown in Figure 2.31.

Figure 2.31: All Cycles in a Simple Directed Graph

cycle	order	node
1	1	A
1	2	B
1	3	C
1	4	A
2	1	A
2	2	E
2	3	B
2	4	C
2	5	A
3	1	A
3	2	E
3	3	C
3	4	A
4	1	B
4	2	C
4	3	D
4	4	E
4	5	B
5	1	B
5	2	C
5	3	D
5	4	F
5	5	E
5	6	B
6	1	E
6	2	C
6	3	D
6	4	E
7	1	E
7	2	C
7	3	D
7	4	F
7	5	E

The six additional cycles are shown graphically in Figure 2.32 through Figure 2.34.

Figure 2.32: Cycles

Figure 2.33: Cycles

Figure 2.34: Cycles