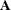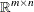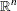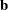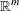The Linear Programming Solver
- Overview
- Getting Started
-
Syntax

-
Details
 PresolvePricing Strategies for the Primal and Dual Simplex AlgorithmsThe Network Simplex AlgorithmThe Interior Point AlgorithmIteration Log for the Primal and Dual Simplex AlgorithmsIteration Log for the Network Simplex AlgorithmIteration Log for the Interior Point AlgorithmIteration Log for the Crossover AlgorithmConcurrent LPParallel ProcessingProblem StatisticsVariable and Constraint StatusIrreducible Infeasible SetMacro Variable _OROPTMODEL_
PresolvePricing Strategies for the Primal and Dual Simplex AlgorithmsThe Network Simplex AlgorithmThe Interior Point AlgorithmIteration Log for the Primal and Dual Simplex AlgorithmsIteration Log for the Network Simplex AlgorithmIteration Log for the Interior Point AlgorithmIteration Log for the Crossover AlgorithmConcurrent LPParallel ProcessingProblem StatisticsVariable and Constraint StatusIrreducible Infeasible SetMacro Variable _OROPTMODEL_ -
Examples
 Diet ProblemReoptimizing the Diet Problem Using BASIS=WARMSTARTTwo-Person Zero-Sum GameFinding an Irreducible Infeasible SetUsing the Network Simplex AlgorithmMigration to OPTMODEL: Generalized NetworksMigration to OPTMODEL: Maximum FlowMigration to OPTMODEL: Production, Inventory, DistributionMigration to OPTMODEL: Shortest Path
Diet ProblemReoptimizing the Diet Problem Using BASIS=WARMSTARTTwo-Person Zero-Sum GameFinding an Irreducible Infeasible SetUsing the Network Simplex AlgorithmMigration to OPTMODEL: Generalized NetworksMigration to OPTMODEL: Maximum FlowMigration to OPTMODEL: Production, Inventory, DistributionMigration to OPTMODEL: Shortest Path - References
Overview: LP Solver
The OPTMODEL procedure provides a framework for specifying and solving linear programs (LPs). A standard linear program has the following formulation:
![\[ \begin{array}{rl} \displaystyle \mathop {\min } & \mathbf{c}^\mr {T} \mathbf{x} \\ \mbox{subject to} & \mathbf{A} \mathbf{x}\; \{ \ge , =, \le \} \; \mathbf{b} \\ & \mathbf{l} \le \mathbf{x} \le \mathbf{u} \end{array} \]](images/ormpug_lpsolver0001.png)
where
|
|
|
|
is the vector of decision variables |
|
|
|
|
is the matrix of constraints |
|
|
|
|
is the vector of objective function coefficients |
|
|
|
|
is the vector of constraints right-hand sides (RHS) |
|
|
|
|
is the vector of lower bounds on variables |
|
|
|
|
is the vector of upper bounds on variables |
The following LP algorithms are available in the OPTMODEL procedure:
-
primal simplex algorithm
-
dual simplex algorithm
-
network simplex algorithm
-
interior point algorithm
The primal and dual simplex algorithms implement the two-phase simplex method. In phase I, the algorithm tries to find a feasible solution. If no feasible solution is found, the LP is infeasible; otherwise, the algorithm enters phase II to solve the original LP. The network simplex algorithm extracts a network substructure, solves this using network simplex, and then constructs an advanced basis to feed to either primal or dual simplex. The interior point algorithm implements a primal-dual predictor-corrector interior point algorithm. If any of the decision variables are constrained to be integer-valued, then the relaxed version of the problem is solved.