The Linear Programming Solver
- Overview
- Getting Started
-
Syntax

-
Details
 PresolvePricing Strategies for the Primal and Dual Simplex AlgorithmsThe Network Simplex AlgorithmThe Interior Point AlgorithmIteration Log for the Primal and Dual Simplex AlgorithmsIteration Log for the Network Simplex AlgorithmIteration Log for the Interior Point AlgorithmIteration Log for the Crossover AlgorithmConcurrent LPParallel ProcessingProblem StatisticsVariable and Constraint StatusIrreducible Infeasible SetMacro Variable _OROPTMODEL_
PresolvePricing Strategies for the Primal and Dual Simplex AlgorithmsThe Network Simplex AlgorithmThe Interior Point AlgorithmIteration Log for the Primal and Dual Simplex AlgorithmsIteration Log for the Network Simplex AlgorithmIteration Log for the Interior Point AlgorithmIteration Log for the Crossover AlgorithmConcurrent LPParallel ProcessingProblem StatisticsVariable and Constraint StatusIrreducible Infeasible SetMacro Variable _OROPTMODEL_ -
Examples
 Diet ProblemReoptimizing the Diet Problem Using BASIS=WARMSTARTTwo-Person Zero-Sum GameFinding an Irreducible Infeasible SetUsing the Network Simplex AlgorithmMigration to OPTMODEL: Generalized NetworksMigration to OPTMODEL: Maximum FlowMigration to OPTMODEL: Production, Inventory, DistributionMigration to OPTMODEL: Shortest Path
Diet ProblemReoptimizing the Diet Problem Using BASIS=WARMSTARTTwo-Person Zero-Sum GameFinding an Irreducible Infeasible SetUsing the Network Simplex AlgorithmMigration to OPTMODEL: Generalized NetworksMigration to OPTMODEL: Maximum FlowMigration to OPTMODEL: Production, Inventory, DistributionMigration to OPTMODEL: Shortest Path - References
Example 7.4 Finding an Irreducible Infeasible Set
This example demonstrates the use of the IIS= option to locate an irreducible infeasible set. Suppose you want to solve a linear program that has the following simple formulation:
![\[ \begin{array}{rllllllcrc} \mbox{min} & & x_1 & + & x_2 & + & x_3 & & & (\mbox{cost})\\ \mbox{ subject to }& & x_1 & + & x_2 & & & \geq & 10 & (\mbox{con1})\\ & & x_1 & & & + & x_3 & \leq & 4 & (\mbox{con2})\\ & 4 \leq & & & x_2 & + & x_3 & \leq & 5 & (\mbox{con3})\\ & & & & & x_1, & x_2 & \geq & 0 & \\ & & & & 0 & \leq & x_3 & \leq & 3 & \\ \end{array} \]](images/ormpug_lpsolver0077.png)
It is easy to verify that the following three constraints (or rows) and one variable (or column) bound form an IIS for this problem:
![\[ \begin{array}{lllllcrc} x_1 & + & x_2 & & & \geq & 10 & (\mbox{con1})\\ x_1 & & & + & x_3 & \leq & 4 & (\mbox{con2})\\ & & x_2 & + & x_3 & \leq & 5 & (\mbox{con3})\\ & & & & x_3 & \geq & 0 & \\ \end{array} \]](images/ormpug_lpsolver0078.png)
You can formulate the problem and call the LP solver by using the following statements:
proc optmodel presolver=none;
/* declare variables */
var x{1..3} >=0;
/* upper bound on variable x[3] */
x[3].ub = 3;
/* objective function */
min obj = x[1] + x[2] + x[3];
/* constraints */
con c1: x[1] + x[2] >= 10;
con c2: x[1] + x[3] <= 4;
con c3: 4 <= x[2] + x[3] <= 5;
solve with lp / iis = on;
print x.status;
print c1.status c2.status c3.status;
The notes printed in the log appear in Output 7.4.1.
Output 7.4.1: Finding an IIS: Log
| NOTE: Problem generation will use 4 threads. |
| NOTE: The problem has 3 variables (0 free, 0 fixed). |
| NOTE: The problem has 3 linear constraints (1 LE, 0 EQ, 1 GE, 1 range). |
| NOTE: The problem has 6 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The IIS= option is enabled. |
| Objective |
| Phase Iteration Value Time |
| P 1 1 1.400000E+01 0 |
| P 1 3 1.000000E+00 0 |
| NOTE: Applying the IIS sensitivity filter. |
| NOTE: The sensitivity filter removed 1 constraints and 3 variable bounds. |
| NOTE: Applying the IIS deletion filter. |
| NOTE: Processing constraints. |
| Processed Removed Time |
| 0 0 0 |
| 1 0 0 |
| 2 0 0 |
| 3 0 0 |
| NOTE: Processing variable bounds. |
| Processed Removed Time |
| 0 0 0 |
| 1 0 0 |
| 2 0 0 |
| 3 0 0 |
| NOTE: The deletion filter removed 0 constraints and 0 variable bounds. |
| NOTE: The IIS= option found this problem to be infeasible. |
| NOTE: The IIS= option found an irreducible infeasible set with 1 variables and |
| 3 constraints. |
| NOTE: The IIS solve time is 0.00 seconds. |
The output of the PRINT statements appears in Output 7.4.2. The value of the .status suffix for the variables x[1] and x[2] is missing, so the variable bounds for x[1] and x[2] are not in the IIS.
Output 7.4.2: Solution Summary, Variable Status, and Constraint Status
The value of c3.status is I_U, which indicates that 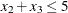 is an element of the IIS. The original constraint is c3, a range constraint with a lower bound of 4. If you choose to remove
the constraint
is an element of the IIS. The original constraint is c3, a range constraint with a lower bound of 4. If you choose to remove
the constraint 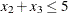 , you can change the value of
, you can change the value of c3.ub to the largest positive number representable in your operating environment. You can specify this number by using the CONSTANT
function.
The modified LP problem is specified and solved by adding the following lines to the original PROC OPTMODEL call.
/* relax upper bound on constraint c3 */
c3.ub = constant('BIG');
solve with lp / iis = on;
Because one element of the IIS has been removed, the modified LP problem should no longer contain the infeasible set. Due to the size of this problem, there should be no additional irreducible infeasible sets.
The notes shown in Output 7.4.3 are printed to the log.
Output 7.4.3: Infeasibility Removed: Log
| NOTE: Problem generation will use 4 threads. |
| NOTE: The problem has 3 variables (0 free, 0 fixed). |
| NOTE: The problem has 3 linear constraints (1 LE, 0 EQ, 2 GE, 0 range). |
| NOTE: The problem has 6 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The IIS= option is enabled. |
| Objective |
| Phase Iteration Value Time |
| P 1 1 1.400000E+01 0 |
| P 1 3 0.000000E+00 0 |
| NOTE: The IIS= option found this problem to be feasible. |
| NOTE: The IIS solve time is 0.00 seconds. |
The solution summary and primal solution are displayed in Output 7.4.4.
Output 7.4.4: Infeasibility Removed: Solution