The Constraint Programming Solver
LEXICO Predicate
-
LEXICO (variable-list order-type variable-list)
The LEXICO predicate defines a lexicographic ordering constraint, which compares two arrays of the same size from left to right. For example, a standings table in a sports competition is usually ordered lexicographically, with certain attributes (such as wins or points) to the left of others (such as goal difference).
The order-type can be either 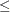 , to indicate lexicographically less than or equal to (
, to indicate lexicographically less than or equal to (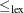 ), or
), or 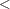 , to indicate lexicographically less than (
, to indicate lexicographically less than (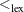 ). Given two n-tuples
). Given two n-tuples 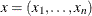 and
and 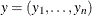 , the n-tuple x is lexicographically less than or equal to y (
, the n-tuple x is lexicographically less than or equal to y (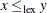 ) if and only if
) if and only if
![\[ \bigl (x_ i = y_ i \: \forall i = 1, \dots , n\bigr ) \vee \left(\exists j \mbox{ with } 1 \leq j \leq n \mbox{ s.t. } x_ i = y_ i \: \forall i = 1, \dots , j\! -\! 1 \mbox{ and } x_ j < y_ j\right) \]](images/ormpug_clpsolver0041.png)
The n-tuple x is lexicographically less than y (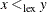 ) if and only if
) if and only if 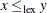 and
and 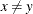 . Equivalently,
. Equivalently, 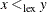 if and only if
if and only if
![\[ \exists j \mbox{ with } 1 \leq j \leq n \mbox{ s.t. } x_ i = y_ i \: \forall i = 1, \dots , j\! -\! 1 \mbox{ and } x_ j < y_ j \]](images/ormpug_clpsolver0044.png)
Informally, you can think of the lexicographic constraint 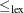 as sorting the n-tuples in alphabetical order. Mathematically,
as sorting the n-tuples in alphabetical order. Mathematically, 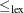 is a partial order on a subset of n-tuples, and
is a partial order on a subset of n-tuples, and 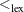 is a strict partial order on a subset of n-tuples (Brualdi 2010).
is a strict partial order on a subset of n-tuples (Brualdi 2010).
For example, you can express the lexicographic constraint ![${(X[1],\dots , X[6]) \le _{\mr{lex}} (Y[1],\dots , Y[6])}$](images/ormpug_clpsolver0045.png) by using a LEXICO predicate as follows:
by using a LEXICO predicate as follows:
con Mycon: lexico({j in 1..6} X[j] <= {j in 1..6} Y[j]);
The assignment ![${X[1]\! =\! 1}$](images/ormpug_clpsolver0046.png) ,
, ![${X[2]\! =\! 2}$](images/ormpug_clpsolver0047.png) ,
, ![${X[3]\! =\! 2}$](images/ormpug_clpsolver0048.png) ,
, ![${X[4]\! =\! 1}$](images/ormpug_clpsolver0049.png) ,
, ![${X[5]\! =\! 2}$](images/ormpug_clpsolver0050.png) ,
, ![${X[6]\! =\! 5}$](images/ormpug_clpsolver0051.png) ,
, ![${Y[1]\! =\! 1}$](images/ormpug_clpsolver0052.png) ,
, ![${Y[2]\! =\! 2}$](images/ormpug_clpsolver0053.png) ,
, ![${Y[3]\! =\! 2}$](images/ormpug_clpsolver0054.png) ,
, ![${Y[4]\! =\! 1}$](images/ormpug_clpsolver0055.png) ,
, ![${Y[5]\! =\! 4}$](images/ormpug_clpsolver0056.png) , and
, and ![${Y[6]\! =\! 3}$](images/ormpug_clpsolver0057.png) satisfies this constraint because
satisfies this constraint because ![$X[i] = Y[i]$](images/ormpug_clpsolver0058.png) for
for 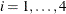 and
and ![$X[5] < Y[5]$](images/ormpug_clpsolver0060.png) . The fact that
. The fact that ![$X[6] > Y[6]$](images/ormpug_clpsolver0061.png) is irrelevant in this ordering.
is irrelevant in this ordering.
Lexicographic ordering constraints can be useful for breaking a certain type of symmetry that arises in CSPs and involves
matrices of decision variables. Frisch et al. (2002) introduce an optimal algorithm to establish generalized arc consistency (GAC) for the 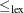 constraint between two vectors of variables.
constraint between two vectors of variables.
