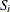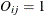The Constraint Programming Solver

This problem is an instance of a category of problems known as the car sequencing problem. A considerable amount of literature discusses this problem (Dincbas, Simonis, and Van Hentenryck 1988; Gravel, Gagne, and Price 2005; Solnon et al. 2008).

A number of cars are to be produced on an assembly line. Each car is customized to include a specific set of options, such as air conditioning, a sunroof, a navigation system, and so on. The assembly line moves through several workstations for installation of these options. The cars cannot be positioned randomly, because each workstation has limited capacity and needs time to set itself up to install the options as the car moves in front of the station. These capacity constraints are formalized using constraints of the form m out of N, which indicates that the workstation can install the option on m out of every sequence of N cars. The car sequencing problem is to determine a sequencing of the cars on the assembly line that satisfies the demand constraints for each set of car options and the capacity constraints for each workstation.

This example comes from Dincbas, Simonis, and Van Hentenryck (1988). Ten cars need to be customized with five possible options. A class of car is defined by a specific set of options; there are six classes of cars.

The data are presented in Table 6.6.

For example, car class 4 requires installation of option 2 and option 4, and two cars of this class are required. The workstation for option 2 can process only two out of every sequence of three cars. The workstation for option 4 has even less capacity—two out of every five cars.

The data for this problem are used to create a SAS data set, which drives the generation of variables and constraints in PROC OPTMODEL.

The decision variables for this problem are shown in Table 6.7.

The following SAS statements express the workstation capacity constraints by using a set of linear constraints for each workstation. A single GCC constraint expresses the demand constraints for each car class. An element constraint for each option variable expresses the relationships between slot variables and option variables.

This model also includes a set of redundant constraints, in the sense that the preceding logical constraints correctly represent the set of feasible solutions. However, the redundant constraints provide the solver with further information specific to this problem, significantly improving the efficiency of domain propagation. Redundant constraints are a core fixture of CLP models. They can determine whether a model will linger and be unsolvable for real data or will produce instant results.

The idea behind the redundant constraint in this model is the following realization: if the workstation for option j has capacity r out of s, then at most r cars in the sequence 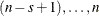can have option j, where n is the total number of cars. Consequently, at least 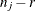cars in the sequence 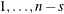must have option j, where 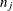is the number of cars that have option j. Generalizing this further, at least 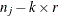cars in the sequence 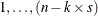must have option j, .

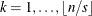data class_data;
   input class cars_cls;
   datalines;
1 1
2 1
3 2
4 2
5 2
6 2
;

data option_data;
   input option max blSz class1-class6;
   datalines;
1 1 2 1 0 0 0 1 1
2 2 3 0 0 1 1 0 1
3 1 3 1 0 0 0 1 0
4 2 5 1 1 0 1 0 0
5 1 5 0 0 1 0 0 0
;

%macro car_sequencing(outdata);
   proc optmodel;
      set CLASSES;
      num nClasses = card(CLASSES);
      num cars_cls {CLASSES};
      read data class_data into CLASSES=[class] cars_cls;

      set OPTIONS;
      num max {OPTIONS};
      num blSz {OPTIONS};
      num list {OPTIONS, CLASSES};
      num cars_opt {i in OPTIONS} = sum {k in CLASSES} cars_cls[k] * list[i,k];
      read data option_data into OPTIONS=[option] max blSz
         {k in CLASSES} <list[option,k]=col('class'||k)>;

      num nCars = sum {k in CLASSES} cars_cls[k];
      set SLOTS = 1..nCars;

      /* Declare Variables */
      /* Slot variables: S[i] - class of car assigned to Slot i */
      var S {SLOTS} integer >= 1 <= nClasses;

      /* Option variables: O[i,j]
      - indicates if class assigned to Slot i needs Option j */
      var O {SLOTS, OPTIONS} binary;

      /* Capacity Constraints: for each option j */
      /* Install in at most max[j] out of every sequence of blSz[j] cars */
      con CapacityCon {j in OPTIONS, i in 0..(nCars-blSz[j])}:
         sum {k in 1..blSz[j]} O[i+k,j] <= max[j];

      /* Demand Constraints: for each class k */
      /* Exactly cars_cls[k] cars */
      con MeetDemandCon:
         gcc(S, setof{k in CLASSES} <k,cars_cls[k],cars_cls[k]>);

      /* Element Constraints: For each slot i and each option j */
      /* relate the slot variable to the option variables.      */
      /* O[i,j] = list[j,S[i]]                                  */
      con OptionsAtSlotCon {i in SLOTS, j in OPTIONS}:
         element(S[i], {k in CLASSES} list[j,k], O[i,j]);

      /* Redundant Constraints to improve efficiency - for every  */
      /*    option j.                                             */
      /* At most max[j] out of every sequence of blSz[j] cars     */
      /*    requires option j.                                    */
      /* All the other slots contain at least cars_opt[j] - max[j]*/
      /*    cars with option j                                    */
      con BoundRemainingCon {j in OPTIONS, i in 1..(nCars/blSz[j])}:
         sum {k in 1..(nCars-i*blSz[j])} O[k,j] >= cars_opt[j] - i * max[j];

      solve with CLP / varselect=minrmaxc findall;

      /* Replicate typical PROC CLP output from PROC OPTMODEL arrays */
      create data &outdata.(drop=sol) from [sol]=(1.._NSOL_)
         {i in SLOTS} <col('S_'||i)=S[i].sol[sol]>
         {i in SLOTS, j in OPTIONS} <col('O_'||i||'_'||j)=O[i,j].sol[sol]>;
   quit;
%mend;
%car_sequencing(sequence_out);

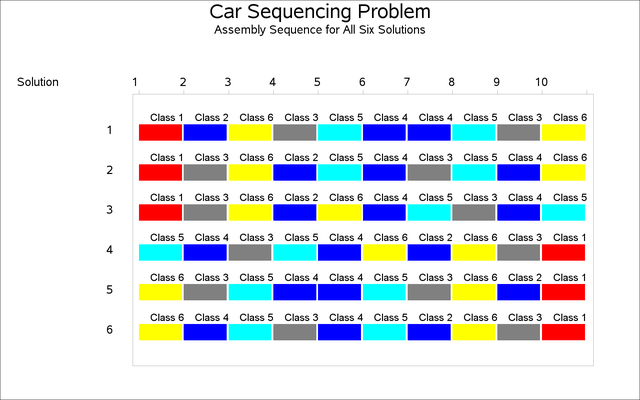
This problem has six solutions, as shown in Output 6.7.1.