The Constraint Programming Solver

Example 6.6 Scene Allocation Problem

The scene allocation problem consists of deciding when to shoot each scene of a movie in order to minimize the total production cost (Van Hentenryck 2002). Each scene involves a number of actors, and at most five scenes a day can be shot. All actors who appear in a scene must be present in the studio on the day the scene is shot. Each actor earns a daily rate for each day spent in the studio, regardless of the number of scenes in which he or she appears on that day. The goal is to shoot the movie for the lowest possible production cost.

The actors’ names, their daily fees, and the scenes in which they appear are contained in the Scene data set, which is shown in Output 6.6.1. The data set variables S_Var1, …, S_Var9 indicate the scenes in which the actor appears. For example, the first observation indicates that Patt’s daily fee is 26,481 and that Patt appears in scenes 2, 5, 7, 10, 11, 13, 15, and 17.

Output 6.6.1: Scene Data Set

Obs	Number	Actor	DailyFee	S_Var1	S_Var2	S_Var3	S_Var4	S_Var5	S_Var6	S_Var7	S_Var8	S_Var9
1	1	Patt	26481	2	5	7	10	11	13	15	17	.
2	2	Casta	25043	4	7	9	10	13	16	19	.	.
3	3	Scolaro	30310	3	6	9	10	14	16	17	18	.
4	4	Murphy	4085	2	8	12	13	15	.	.	.	.
5	5	Brown	7562	2	3	12	17	.	.	.	.	.
6	6	Hacket	9381	1	2	12	13	18	.	.	.	.
7	7	Anderson	8770	5	6	14	.	.	.	.	.	.
8	8	McDougal	5788	3	5	6	9	10	12	15	16	18
9	9	Mercer	7423	3	4	5	8	9	16	.	.	.
10	10	Spring	3303	5	6	.	.	.	.	.	.	.
11	11	Thompson	9593	6	9	12	15	18	.	.	.	.

There are 19 scenes. At most 5 scenes can be filmed in one day, so at least four days are needed to schedule all the scenes (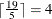 $\lceil \frac{19}{5} \rceil =4$ ). Let 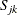$S_{jk}$ be a binary variable that equals 1 if scene j is shot on day k. Let 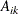$A_{ik}$ be another binary variable that equals 1 if actor i is present on day k. The input daily_fee $_ i$ is the daily cost of the ith actor.

The objective function that represents the total production cost is

$\min \sum _{i=1}^{11}\sum _{k=1}^4 {\mathrm{daily\_ fee}_ i \times A_{ik} }$

This example illustrates the use of symmetry-breaking constraints. In this model, the “1” in day 1 does not refer to sequence but simply to the label of the day. Thus, you can call day 1 the day on which scene 1 is shot, whichever day that is. Similarly, either scene 2 is shot on the same day as scene 1 (day 1) or it is shot on another day, which you can call day 2. Scene 3 is shot either on one of those two days or on another day. Adding constraints that eliminate symmetry can significantly improve the performance of a CLP model. In this model, the symmetry-breaking constraints prevent the solver from considering three other assignments that do not differ in any meaningful way.

The following PROC OPTMODEL statements implement these ideas:

proc optmodel;
   set ACTORS;
   str actor_name {ACTORS};
   num daily_fee {ACTORS};
   num most_scenes = 9; /* most scenes by any actor */
   num scene_list {ACTORS, 1..most_scenes};
   read data scene into ACTORS=[_N_]
      actor_name=Actor daily_fee=DailyFee
      {j in 1..most_scenes} <scene_list[_N_,j]=col('S_Var'||j)>;
   print actor_name daily_fee scene_list;

   set SCENES_actor {i in ACTORS} =
      (setof {j in 1..most_scenes} scene_list[i,j]) diff {.};
   set SCENES = 1..19;
   set DAYS = 1..4;

   /* Indicates if actor i is present on day k. */
   var A {ACTORS, DAYS} binary;

   /* Indicates if scene j is shot on day k. */
   var S {SCENES, DAYS} binary;

   /* Every scene is shot exactly once.*/
   con SceneCon {j in SCENES}:
      gcc({k in DAYS} S[j,k], {<1,1,1>});

   /* At least 4 and at most 5 scenes are shot per day. */
   con NumScenesPerDayCon {k in DAYS}:
      gcc({j in SCENES} S[j,k], {<1,4,5>});

   /* Actors for a scene must be present on day of shooting. */
   con LinkCon {i in ACTORS, j in SCENES_actor[i], k in DAYS}:
      S[j,k] <= A[i,k];

   /* symmetry-breaking constraints. Without loss of any generality, we
      can assume Scene1 to be shot on day 1, Scene2 to be shot on day 1
      or day 2, and Scene3 to be shot on either day 1, day 2, or day 3.  */
   fix S[1,1] = 1;
   for {k in 2..4} fix S[1,k] = 0;
   for {k in 3..4} fix S[2,k] = 0;
   fix S[3,4] = 0;

   /* If Scene2 is shot on day 1, (as opposed to day 2) */
   /* then Scene3 can be shot on day 1 or day 2 (but not day 3). */
   con Symmetry:
      S[2,1] + S[3,3] <= 1;

   /* Minimize total cost. */
   min TotalCost = sum {i in ACTORS, k in DAYS} daily_fee[i] * A[i,k];

   /* Set lower and upper bounds for the objective value   */
   /* Lower bound: every actor appears on one day.         */
   /* Upper bound: every actor appears on all four days.   */
   num obj_lb = sum {i in ACTORS} daily_fee[i];
   num obj_ub = sum {i in ACTORS, k in DAYS} daily_fee[i];
   put obj_lb= obj_ub=;
   con TotalCost_bounds:
      obj_lb <= TotalCost <= obj_ub;

   solve with CLP / varselect=maxc;
quit;

The optimal production cost is 334,144, as reported in the _OROPTMODEL_ macro variable. The corresponding actor schedules and scene schedules are displayed in Output 6.6.2 and Output 6.6.3, respectively.

Output 6.6.2: Scene Allocation Problem: Actor Schedules

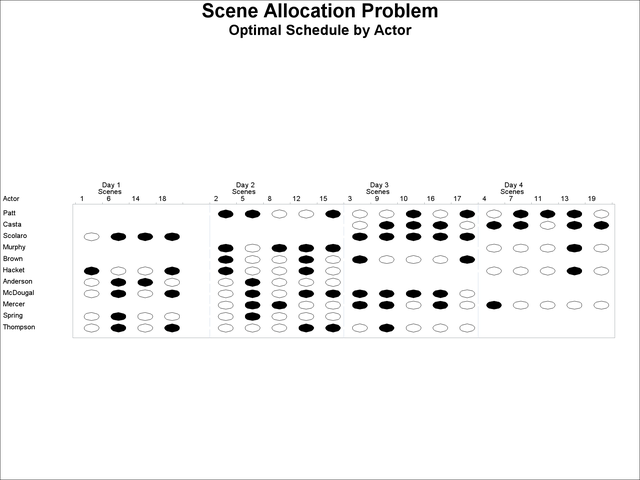
Output 6.6.3: Scene Allocation Problem: Scene Schedules