The Nonlinear Programming Solver
Constrained Optimization
A function that plays a pivotal role in establishing conditions that characterize a local minimum of an NLP problem is the
Lagrangian function ![]() , which is defined as
, which is defined as
|
|
Note that the Lagrangian function can be seen as a linear combination of the objective and constraint functions. The coefficients
of the constraints, ![]() , and
, and ![]() , are called the Lagrange multipliers or dual variables. At a feasible point
, are called the Lagrange multipliers or dual variables. At a feasible point ![]() , an inequality constraint is called active if it is satisfied as an equality—that is,
, an inequality constraint is called active if it is satisfied as an equality—that is, ![]() . The set of active constraints at a feasible point
. The set of active constraints at a feasible point ![]() is then defined as the union of the index set of the equality constraints,
is then defined as the union of the index set of the equality constraints, ![]() , and the indices of those inequality constraints that are active at
, and the indices of those inequality constraints that are active at ![]() ; that is,
; that is,
|
|
An important condition that is assumed to hold in the majority of optimization algorithms is the so-called linear independence
constraint qualification (LICQ). The LICQ states that at any feasible point ![]() , the gradients of all the active constraints are linearly independent. The main purpose of the LICQ is to ensure that the
set of constraints is well-defined in a way that there are no redundant constraints or in a way that there are no constraints
defined such that their gradients are always equal to zero.
, the gradients of all the active constraints are linearly independent. The main purpose of the LICQ is to ensure that the
set of constraints is well-defined in a way that there are no redundant constraints or in a way that there are no constraints
defined such that their gradients are always equal to zero.
The First-Order Necessary Optimality Conditions
If ![]() is a local minimum of the NLP problem and the LICQ holds at
is a local minimum of the NLP problem and the LICQ holds at ![]() , then there are vectors of Lagrange multipliers
, then there are vectors of Lagrange multipliers ![]() and
and ![]() , with components
, with components ![]() , and
, and ![]() , respectively, such that the following conditions are satisfied:
, respectively, such that the following conditions are satisfied:
![\[ \begin{array}{rclr} \nabla _{x} \mathcal{L}(x^{*}, y^{*}, z^{*}) & =& 0 & \\ h_{i}(x^{*}) & =& 0, & i \in \mathcal{E} \\ g_{i}(x^{*}) & \ge & 0, & i \in \mathcal{I} \\ z_{i}^{*} & \ge & 0, & i \in \mathcal{I} \\ z_{i}^{*} g_{i}(x^{*}) & =& 0, & i \in \mathcal{I} \end{array} \]](images/ormpug_nlpsolver0063.png) |
where ![]() is the gradient of the Lagrangian function with respect to x, defined as
is the gradient of the Lagrangian function with respect to x, defined as
|
|
The preceding conditions are often called the Karush-Kuhn-Tucker (KKT) conditions. The last group of equations (![]() ) is called the complementarity condition. Its main aim is to try to force the Lagrange multipliers,
) is called the complementarity condition. Its main aim is to try to force the Lagrange multipliers, ![]() , of the inactive inequalities (that is, those inequalities with
, of the inactive inequalities (that is, those inequalities with ![]() ) to zero.
) to zero.
The KKT conditions describe the way the first derivatives of the objective and constraints are related at a local minimum
![]() . However, they are not enough to fully characterize a local minimum. The second-order optimality conditions attempt to fulfill
this aim by examining the curvature of the Hessian matrix of the Lagrangian function at a point that satisfies the KKT conditions.
. However, they are not enough to fully characterize a local minimum. The second-order optimality conditions attempt to fulfill
this aim by examining the curvature of the Hessian matrix of the Lagrangian function at a point that satisfies the KKT conditions.
The Second-Order Necessary Optimality Condition
Let ![]() be a local minimum of the NLP problem, and let
be a local minimum of the NLP problem, and let ![]() and
and ![]() be the corresponding Lagrange multipliers that satisfy the first-order optimality conditions. Then
be the corresponding Lagrange multipliers that satisfy the first-order optimality conditions. Then ![]() for all nonzero vectors d that satisfy the following conditions:
for all nonzero vectors d that satisfy the following conditions:
-
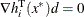 ,
, 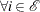
-
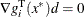 ,
, 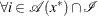 , such that
, such that 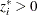
-
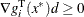 ,
, 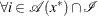 , such that
, such that 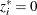
The second-order necessary optimality condition states that, at a local minimum, the curvature of the Lagrangian function along the directions that satisfy the preceding conditions must be nonnegative.
