The OPTLP Procedure

Data Input and Output

This subsection describes the PRIMALIN= and DUALIN= data sets required to warm start the primal and dual simplex solvers, and the PRIMALOUT= and DUALOUT= output data sets.

Definitions of Variables in the PRIMALIN= Data Set

The PRIMALIN= data set has two required variables defined as follows:

_VAR_

specifies the name of the decision variable.

_STATUS_

specifies the status of the decision variable. It can take one of the following values:

B: basic variable
L: nonbasic variable at its lower bound
U: nonbasic variable at its upper bound
F: free variable
A: newly added variable in the modified LP model when using the BASIS=WARMSTART option

Note: The PRIMALIN= data set is created from the PRIMALOUT= data set obtained from a previous "normal" run of PROC OPTLP—i.e., using only the DATA= data set as the input.

Definitions of Variables in the DUALIN= Data Set

The DUALIN= data set also has two required variables defined as follows:

_ROW_

specifies the name of the constraint.

_STATUS_

specifies the status of the slack variable for a given constraint. It can take one of the following values:

B: basic variable
L: nonbasic variable at its lower bound
U: nonbasic variable at its upper bound
F: free variable
A: newly added variable in the modified LP model when using the BASIS=WARMSTART option

Note: The DUALIN= data set is created from the DUALOUT= data set obtained from a previous "normal" run of PROC OPTLP—i.e., using only the DATA= data set as the input.

Definitions of Variables in the PRIMALOUT= Data Set

The PRIMALOUT= data set contains the primal solution to the LP model; each observation corresponds to a variable of the LP problem. If the SAVE_ONLY_IF_OPTIMAL option is not specified, the PRIMALOUT= data set can contain an intermediate solution, if one is available. See Example 10.1 for an example of the PRIMALOUT= data set. The variables in the data set have the following names and meanings.

_OBJ_ID_

specifies the name of the objective function. This is particularly useful when there are multiple objective functions, in which case each objective function has a unique name.

Note: PROC OPTLP does not support simultaneous optimization of multiple objective functions in this release.

_RHS_ID_

specifies the name of the variable that contains the right-hand-side value of each constraint.

_VAR_

specifies the name of the decision variable.

_TYPE_

specifies the type of the decision variable. _TYPE_ can take one of the following values:

N: nonnegative
D: bounded (with both lower and upper bound)
F: free
X: fixed
O: other (with either lower or upper bound)

_OBJCOEF_

specifies the coefficient of the decision variable in the objective function.

_LBOUND_

specifies the lower bound on the decision variable.

_UBOUND_

specifies the upper bound on the decision variable.

_VALUE_

specifies the value of the decision variable.

_STATUS_

specifies the status of the decision variable. _STATUS_ can take one of the following values:

B: basic variable
L: nonbasic variable at its lower bound
U: nonbasic variable at its upper bound
F: free variable
I: LP model infeasible (all decision variables have _STATUS_ equal to I)

For the interior point solver with IIS= OFF, _STATUS_ is blank.

The following values can appear only if IIS= ON. See the section Irreducible Infeasible Set for details.

I_L: the lower bound of the variable is violated
I_U: the upper bound of the variable is violated
I_F: the fixed bound of the variable is violated

_R_COST_

specifies the reduced cost of the decision variable, which is the amount by which the objective function is increased per unit increase in the decision variable. The reduced cost associated with the 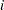$\text{[math]}$ th variable is the 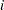$\text{[math]}$ th entry of the following vector: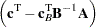

$\text{[math]}$

where 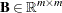$\text{[math]}$ denotes the basis (matrix composed of basic columns of the constraints matrix 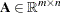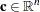$\text{[math]}$ ), $\text{[math]}$ is the vector of objective function coefficients, and 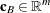$\text{[math]}$ is the vector of objective coefficients of the variables in the basis.

Definitions of Variables in the DUALOUT= Data Set

The DUALOUT= data set contains the dual solution to the LP model; each observation corresponds to a constraint of the LP problem. If the SAVE_ONLY_IF_OPTIMAL option is not specified, the PRIMALOUT= data set can contain an intermediate solution, if one is available. Information about the objective rows of the LP problems is not included. See Example 10.1 for an example of the DUALOUT= data set. The variables in the data set have the following names and meanings.

_OBJ_ID_

specifies the name of the objective function. This is particularly useful when there are multiple objective functions, in which case each objective function has a unique name.

Note: PROC OPTLP does not support simultaneous optimization of multiple objective functions in this release.

_RHS_ID_

specifies the name of the variable that contains the right-hand-side value of each constraint.

_ROW_

specifies the name of the constraint.

_TYPE_

specifies the type of the constraint. _TYPE_ can take one of the following values:

L: "less than or equals" constraint
E: equality constraint
G: "greater than or equals" constraint
R: ranged constraint (both "less than or equals" and "greater than or equals")

_RHS_

specifies the value of the right-hand side of the constraint. It takes a missing value for a ranged constraint.

_L_RHS_

specifies the lower bound of a ranged constraint. It takes a missing value for a non-ranged constraint.

_U_RHS_

specifies the upper bound of a ranged constraint. It takes a missing value for a non-ranged constraint.

_VALUE_

specifies the value of the dual variable associated with the constraint.

_STATUS_

specifies the status of the slack variable for the constraint. _STATUS_ can take one of the following values:

B: basic variable
L: nonbasic variable at its lower bound
U: nonbasic variable at its upper bound
F: free variable
I: LP model infeasible (all decision variables have _STATUS_ equal to I)

The following values can appear only if option IIS= ON. See the section Irreducible Infeasible Set for details.

I_L: the "GE" ( $\text{[math]}$ ) condition of the constraint is violated
I_U: the "LE" ( 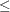$\text{[math]}$ ) condition of the constraint is violated
I_F: the "EQ" ( 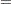$\text{[math]}$ ) condition of the constraint is violated

_ACTIVITY_

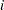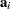specifies the left-hand-side value of a constraint. In other words, the value of _ACTIVITY_ for the $\text{[math]}$ th constraint would be equal to $\text{[math]}$ , where $\text{[math]}$ refers to the 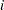$\text{[math]}$ th row of the constraints matrix and $\text{[math]}$ denotes the vector of current decision variable values.

Data Magnitude and Variable Bounds

Extremely large numerical values might cause computational difficulties for the OPTLP procedure, but the occurrence of such difficulties is hard to predict. For this reason, the OPTLP procedure issues a data error message whenever it detects model data that exceeds a specific threshold number. The value of the threshold number depends on your operating environment and is printed in the log as part of the data error message.

The following conditions produce a data error:

The absolute value of an objective coefficient, constraint coefficient, or range (difference between the upper and lower bounds on a constraint) is greater than the threshold number.
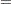A variable’s lower bound, a $\text{[math]}$ or $\text{[math]}$ constraint’s right-hand side, or a range constraint’s lower bound is greater than the threshold number.
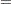A variable’s upper bound, a $\text{[math]}$ or $\text{[math]}$ constraint’s right-hand side, or a range constraint’s upper bound is smaller than the negative threshold number.

If a variable’s upper bound is larger than 1E20, then the OPTLP procedure treats the bound as $\text{[math]}$ . Similarly, if a variable’s lower bound is smaller than –1E20, then the OPTLP procedure treats the bound as $\text{[math]}$ .