The Linear Programming Solver
- Overview
- Getting Started
-
Syntax
-
Details
Presolve Pricing Strategies for the Primal and Dual Simplex Solvers The Network Simplex Algorithm The Interior Point Algorithm Macro Variable OROPTMODEL Iteration Log for the Primal and Dual Simplex Solvers Iteration Log for the Network Simplex Solver Iteration Log for the Interior Point Solver Problem Statistics Data Magnitude and Variable Bounds Variable and Constraint Status Irreducible Infeasible Set
-
Examples
Diet Problem Reoptimizing the Diet Problem Using BASIS=WARMSTART Two-Person Zero-Sum Game Finding an Irreducible Infeasible Set Using the Network Simplex Solver Migration to OPTMODEL: Generalized Networks Migration to OPTMODEL: Maximum Flow Migration to OPTMODEL: Production, Inventory, Distribution Migration to OPTMODEL: Shortest Path
- References
| Irreducible Infeasible Set |
For a linear programming problem, an irreducible infeasible set (IIS) is an infeasible subset of constraints and variable bounds that will become feasible if any single constraint or variable bound is removed. It is possible to have more than one IIS in an infeasible LP. Identifying an IIS can help to isolate the structural infeasibility in an LP.
The IIS=ON option directs the LP solver to search for an IIS in a given LP. The OPTMODEL option PRESOLVER=NONE should be specified when IIS=ON is specified; otherwise, the IIS results can be incomplete. The LP presolver is not applied to the problem during the IIS search. If the LP solver detects an IIS, it updates the .status suffix of the decision variables and constraints, then stops. Otherwise, the problem is sent on to the LP presolver, followed by the specified solver.
The IIS= option can add special values to the .status suffixes of variables and constraints. (See the section Variable and Constraint Status for more information.) For constraints, a status of "I_L", "I_U", or "I_F" indicates, respectively, the "GE" (
), "LE" (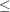
), or "EQ" (
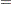) condition is violated. For range constraints, a status of "I_L" or "I_U" indicates, respectively, that the lower or upper bound of the constraint is violated. For variables, a status of "I_L", "I_U", or "I_F" indicates, respectively, the lower, upper, or fixed bound of the variable is violated. From this information, you can identify names of the constraints (variables) in the IIS as well as the corresponding bound where infeasibility occurs.
Making any one of the constraints or variable bounds in the IIS nonbinding will remove the infeasibility from the IIS. In some cases, changing a right-hand side or bound by a finite amount will remove the infeasibility; however, the only way to guarantee removal of the infeasibility is to set the appropriate right-hand side or bound to 
or 
. Since it is possible for an LP to have multiple irreducible infeasible sets, simply removing the infeasibility from one set might not make the entire problem feasible.
See Example 5.4 for an example demonstrating the use of the IIS= option in locating and removing infeasibilities.