| The Interior Point NLP Solver |
Example 9.2 Solving Unconstrained Optimization Problems
Although the IPNLP techniques are suited for solving constrained NLP problems, they can also be used to solve unconstrained problems efficiently. This example demonstrates this solution by considering the relatively large unconstrained NLP problem
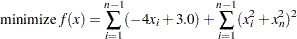 |
where 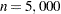 . To solve this problem, you can write the following statements:
. To solve this problem, you can write the following statements:
proc optmodel;
number N=5000;
var x{1..N} init 1.0;
minimize obj = sum {i in 1..N - 1} ( - 4 * x[i] + 3.0) +
sum {i in 1..N - 1} (x[i]^2 + x[N]^2)^2;
solve with ipnlp / tech=ipkrylov;
quit;
The problem and solution summaries are shown in Output 9.2.1. Since the problem contains several thousands of variables, the iterative trust region interior point technique is used (TECH=IPKRYLOV).
This example can also be solved by the quasi-Newton interior point solver (using TECH=IPQN). Since IPQN uses dense linear algebra, more memory than the default needs to be assigned. Additional memory can be assigned by using the MEMSIZE option.
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | obj |
| Objective Type | Nonlinear |
| Number of Variables | 5000 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 0 |
| Free | 5000 |
| Fixed | 0 |
| Number of Constraints | 0 |
Copyright © SAS Institute, Inc. All Rights Reserved.