The Interior Point NLP Solver: Solving NLP Problems with Range Constraints :: SAS/OR(R) 9.22 User's Guide: Mathematical Programming

The Interior Point NLP Solver

Example 9.3 Solving NLP Problems with Range Constraints

Often there are constraints with both lower and upper bounds (that is, 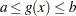$\text{[math]}$ ). These constraints are called range constraints. The IPNLP solver can handle range constraints in an efficient way. Consider the NLP problem

$\text{[math]}$

where the values of the parameters $\text{[math]}$ , are shown in Table 9.2.

Table 9.2 Data for Example 3
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
1	85.334407	5	80.51249	9	0.0047026
2	0.0056858	6	0.0071317	10	0.0012547
3	0.0006262	7	0.0029955	11	0.0019085
4	0.0022053	8	0.0021813	12	0.0019085

The initial point used is 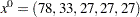$\text{[math]}$ . You can call the IPNLP solver within PROC OPTMODEL to solve this problem by writing the following statements:


proc optmodel;
   number l {1..5} = [78 33 27 27 27];
   number u {1..5} = [102 45 45 45 45];

   number a {1..12} = 
      [85.334407 0.0056858 0.0006262 0.0022053
      80.51249 0.0071317 0.0029955 0.0021813
      9.300961 0.0047026 0.0012547 0.0019085];

   var x {j in 1..5} >= l[j] <= u[j];

   minimize obj = 5.35*x[3]^2 + 0.83*x[1]*x[5] + 37.29*x[1] 
                  - 40792.141;

   con constr1: 
      0 <= a[1] + a[2]*x[2]*x[5] + a[3]*x[1]*x[4] - 
         a[4]*x[3]*x[5] <= 92;
   con constr2: 
      0 <= a[5] + a[6]*x[2]*x[5] + a[7]*x[1]*x[2] + 
         a[8]*x[3]^2 - 90 <= 20;
   con constr3: 
      0 <= a[9] + a[10]*x[3]*x[5] + a[11]*x[1]*x[3] + 
         a[12]*x[3]*x[4] -20 <= 5;

   x[1] = 78;
   x[2] = 33;
   x[3] = 27;
   x[4] = 27;
   x[5] = 27;

   solve with ipnlp / tech=IPQN;
   print x;
quit;

The summaries and optimal solution are shown in Output 9.3.1. Since this problem contains a small number of variables, the quasi-Newton interior point technique is used (TECH=IPQN).

Output 9.3.1 Summaries and the Optimal Solution

The OPTMODEL Procedure

Problem Summary
Objective Sense	Minimization
Objective Function	obj
Objective Type	Quadratic

Number of Variables	5
Bounded Above	0
Bounded Below	0
Bounded Below and Above	5
Free	0
Fixed	0

Number of Constraints	3
Linear LE (<=)	0
Linear EQ (=)	0
Linear GE (>=)	0
Linear Range	0
Nonlinear LE (<=)	0
Nonlinear EQ (=)	0
Nonlinear GE (>=)	0
Nonlinear Range	3

Solution Summary
Solver	IPNLP/IPQN
Objective Function	obj
Solution Status	Optimal
Objective Value	-30689.1889
Iterations	73

Infeasibility	2.664535E-15
Optimality Error	5.9764587E-7

[1]	x
1	78.000
2	33.000
3	29.995
4	45.000
5	36.776

Top of Page