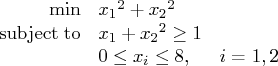Previous Page

|

Next Page

Example 13.2: Using the HESCHECK Option

The following example illustrates how the HESCHECK option could be useful:

Use the following SAS code to solve the problem:

    proc optmodel;
       var x {1..2} <= 8 >= 0   /* variable bounds */
          init 0;   /* starting point */
       
       minimize obj = x[1]^2 + x[2]^2;
       
       con cons: 
          x[1] + x[2]^2 >= 1;
       
       solve with sqp / printfreq = 5;
       print x;
    quit;
 

When = (0, 0) is chosen as the starting point, the SQP solver converges to (1, 0), as displayed in Output 13.2.1. It can be easily verified that (1, 0) is a stationary point and not an optimal solution.

To resolve this issue, you can use the HESCHECK option in the SOLVE statement as follows:

  
    proc optmodel; 
    ... 
       solve with sqp / printfreq = 1 hescheck; 
    ... 
    quit;
 

For the same starting point = (0, 0), the SQP solver now converges to the optimal solution, , as displayed in Output 13.2.2.