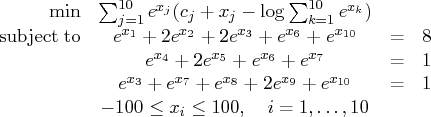Previous Page

|

Next Page

Example 13.1: Solving a Highly Nonlinear Problem

Consider the following example of minimizing a highly nonlinear problem:

In this instance, the constants are . Assume the starting point . You can use the following SAS code to solve the problem:

    proc optmodel;
       var x {1..10} >= -100 <= 100   /* variable bounds */
          init -2.3;   /* starting point */
    
       number c {1..10} = [-6.089 -17.164 -34.054 -5.914 -24.721 
          -14.986 -24.100 -10.708 -26.662 -22.179];
       
       number a{1..3,1..10}=[1 2 2 0 0 1 0 0 0 1
                             0 0 0 1 2 1 1 0 0 0
                             0 0 1 0 0 0 1 1 2 1];
       
       number b{1..3}=[8 1 1];
       
       minimize obj = 
          sum{j in 1..10}exp(x[j])*(c[j]+x[j]
             -log(sum {k in 1..10}exp(x[k])));
       
       con cons{i in 1..3}: 
          sum{j in 1..10}a[i,j]*exp(x[j])=b[i];
       
       solve with sqp / printfreq = 0;
    quit;
 

The output is displayed in Output 13.1.1.