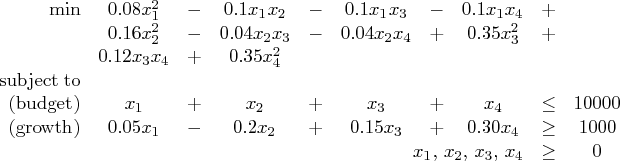PROC OPTQP: Example 17.2: Portfolio Optimization :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The OPTQP Procedure

Example 17.2: Portfolio Optimization

Consider a portfolio optimization example. The two competing goals of investment are (1) long-term growth of capital and (2) low risk. A good portfolio grows steadily without wild fluctuations in value. The Markowitz model is an optimization model for balancing the return and risk of a portfolio. The decision variables are the amounts invested in each asset. The objective is to minimize the variance of the portfolio's total return, subject to the constraints that (1) the expected growth of the portfolio reaches at least some target level and (2) you do not invest more capital than you have.

Let be the amount invested in each asset, $\mathcal{b}$ be the amount of capital you have, $\mathbf{r}$ be the random vector of asset returns over some period, and $\mathbf{r}$ be the expected value of $\mathbf{r}$ . Let be the minimum growth you hope to obtain, and $\mathcal{c}$ be the covariance matrix of $\mathbf{r}$ . The objective function is ${\rm var}( \sum \limits_{i=1}^n x_i r_i )$ , which can be equivalently denoted as $\mathbf{x}^{\rm t} \mathcal{c}\mathbf{x}$ .

Assume, for example, = 4. Let $\mathcal{b}$ = 10,000, = 1000, $\mathbf{r} = [0.05, -0.2, 0.15, 0.30]$ , and

$\mathcal{c} & = & [ 0.08 & -0.05 & -0.05 & -0.05\ -0.05 & 0.16 & -0.02 & -0.02\ -0.05 & -0.02 & 0.35 & 0.06\ -0.05 & -0.02 & 0.06 & 0.35\ ]\$

The QP formulation can be written as follows:

${\min} & 0.08x_1^2 & - & 0.1 x_1 x_2 & - & 0.1 x_1 x_3 & - & 0.1 x_1 x_4 & + & \... ... x_4 & \geq & 1000 \ & \multicolumn{7}r{x_1,\, x_2, \, x_3, \, x_4} & \ge & 0$

The corresponding QPS-format input data set is as follows:

 data portdata;
    input field1 $ field2 $ field3$ field4 field5 $ field6 @;
 datalines;
 NAME  .         PORT     .          .         .       
 ROWS  .         .        .          .         .
 N     OBJ.FUNC  .        .          .         .
 L     BUDGET    .        .          .         .
 G     GROWTH    .        .          .         .
 COLUMNS .       .        .          .         .
 .     X1        BUDGET   1.0        GROWTH    0.05
 .     X2        BUDGET   1.0        GROWTH    -.20
 .     X3        BUDGET   1.0        GROWTH    0.15
 .     X4        BUDGET   1.0        GROWTH    0.30
 RHS   .         .        .          .         .
 .     RHS       BUDGET   10000      .         .
 .     RHS       GROWTH   1000       .         .
 RANGES .        .        .          .         . 
 BOUNDS .        .        .          .         .
 QUADOBJ .        .       .           .        .
 .     X1        X1       0.16       .         . 
 .     X1        X2       -.10       .         .
 .     X1        X3       -.10       .         .
 .     X1        X4       -.10       .         .
 .     X2        X2       0.32       .         .
 .     X2        X3       -.04       .         . 
 .     X2        X4       -.04       .         .
 .     X3        X3       0.70       .         .
 .     X3        X4       0.12       .         .
 .     X4        X4       0.70       .         .
 ENDATA .        .        .          .         .
 ;

Use the following SAS code to solve the problem:

    proc optqp data=portdata 
      primalout = portpout 
      dualout   = portdout;
    run;

The optimal solution is shown in Output 17.2.1.

Output 17.2.1: Portfolio Optimization

The OPTQP Procedure

Primal Solution

Obs	Objective Function ID	RHS ID	Variable Name	Variable Type	Upper Bound	Variable Value	Variable Status
1	OBJ.FUNC	RHS	X1	N	1.7977E308	3452.86	O
2	OBJ.FUNC	RHS	X2	N	1.7977E308	0.00	O
3	OBJ.FUNC	RHS	X3	N	1.7977E308	1068.81	O
4	OBJ.FUNC	RHS	X4	N	1.7977E308	2223.45	O

Thus, the minimum variance portfolio that earns an expected return of at least 10% is , , , . Asset 2 gets nothing, because its expected return is -20% and its covariance with the other assets is not sufficiently negative for it to bring any diversification benefits. What if we drop the nonnegativity assumption? You need to update the BOUNDS section in the existing QPS-format data set to indicate that the decision variables are free.

  
    ... 
    RANGES .        .        .          .         . 
    BOUNDS .        .        .          .         . 
    FR    BND1      X1       .          .         . 
    FR    BND1      X2       .          .         . 
    FR    BND1      X3       .          .         . 
    FR    BND1      X4       .          .         . 
    QUADOBJ .        .       .          .         . 
    ...

Financially, that means you are allowed to short-sell - i.e., sell low-mean-return assets and use the proceeds to invest in high-mean-return assets. In other words, you put a negative portfolio weight in low-mean assets and "more than 100%" in high-mean assets. You can see in the optimal solution displayed in Output 17.2.2 that the decision variable , denoting Asset 2, is equal to -1563.61, which means short sale of that asset.

Output 17.2.2: Portfolio Optimization with Short-Sale Option

The OPTQP Procedure

Primal Solution

Obs	Objective Function ID	RHS ID	Variable Name	Variable Type	Lower Bound	Upper Bound	Variable Value	Variable Status
1	OBJ.FUNC	RHS	X1	F	-1.7977E308	1.7977E308	1684.35	O
2	OBJ.FUNC	RHS	X2	F	-1.7977E308	1.7977E308	-1563.61	O
3	OBJ.FUNC	RHS	X3	F	-1.7977E308	1.7977E308	682.51	O
4	OBJ.FUNC	RHS	X4	F	-1.7977E308	1.7977E308	1668.95	O

Top of Page