The NLP Procedure

Computational Problems

First Iteration Overflows

If you use bad initial values for the parameters, the computation of the value of the objective function (and its derivatives) can lead to arithmetic overflows in the first iteration. The line-search algorithms that work with cubic extrapolation are especially sensitive to arithmetic overflows. If an overflow occurs with an optimization technique that uses line search, you can use the INSTEP= option to reduce the length of the first trial step during the line search of the first five iterations or use the DAMPSTEP or MAXSTEP= option to restrict the step length of the initial in subsequent iterations. If an arithmetic overflow occurs in the first iteration of the trust region, double dogleg, or Levenberg-Marquardt algorithm, you can use the INSTEP= option to reduce the default trust region radius of the first iteration. You can also change the minimization technique or the line-search method. If none of these methods helps, consider the following actions:

• scale the parameters
• provide better initial values
• use boundary constraints to avoid the region where overflows may happen
• change the algorithm (specified in program statements) which computes the objective function

Problems in Evaluating the Objective Function

The starting point must be a point that can be evaluated by all the functions involved in your problem. However, during optimization the optimizer may iterate to a point where the objective function or nonlinear constraint functions and their derivatives cannot be evaluated. If you can identify the problematic region, you can prevent the algorithm from reaching it by adding another constraint to the problem. Another possibility is a modification of the objective function that will produce a large, undesired function value. As a result, the optimization algorithm reduces the step length and stays closer to the point that has been evaluated successfully in the previous iteration. For more information, refer to the section "Missing Values in Program Statements".

Problems with Quasi-Newton Methods for Nonlinear Constraints

The sequential quadratic programming algorithm in QUANEW, which is used for solving nonlinearly constrained problems, can have problems updating the Lagrange multiplier vector . This usually results in very high values of the Lagrangian function and in watchdog restarts indicated in the iteration history. If this happens, there are three actions you can try:

• By default, the Lagr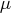ange vector is evaluated in the same way as Powell (1982b) describes. This corresponds to VERSION=2. By specifying VERSION=1, a modification of this algorithm replaces the update of the Lagrange vector 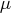with the original update of Powell (1978a,b), which is used in VF02AD.
• You can use the INSTEP= option to impose an upper bound for the step length 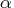during the first five iterations.
• You can use the INHESSIAN= option to specify a different starting approximation for the Hessian. Choosing only the INHESSIAN option will use the Cholesky factor of a (possibly ridged) finite-difference approximation of the Hessian to initialize the quasi-Newton update process.

Other Convergence Difficulties

There are a number of things to try if the optimizer fails to converge.

• Check the derivative specification:
  If derivatives are specified by using the GRADIENT, HESSIAN, JACOBIAN, CRPJAC, or JACNLC statement, you can compare the specified derivatives with those computed by finite-difference approximations (specifying the FD and FDHESSIAN option). Use the GRADCHECK option to check if the gradient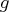 is correct. For more information, refer to the section "Testing the Gradient Specification".
• Forward-difference derivatives specified with the FD= or FDHESSIAN= option may not be precise enough to satisfy strong gradient termination criteria. You may need to specify the more expensive central-difference formulas or use analytical derivatives. The finite-difference intervals may be too small or too big and the finite-difference derivatives may be erroneous. You can specify the FDINT= option to compute better finite-difference intervals.
• Change the optimization technique:
  For example, if you use the default TECH=LEVMAR, you can
  • change to TECH=QUANEW or to TECH=NRRIDG
  • run some iterations with TECH=CONGRA, write the results in an OUTEST= data set, and use them as initial values specified by an INEST= data set in a second run with a different TECH= technique
• Change or modify the update technique and the line-search algorithm:
  This method applies only to TECH=QUANEW, TECH=HYQUAN, or TECH=CONGRA. For example, if you use the default update formula and the default line-search algorithm, you can
  • change the update formula with the UPDATE= option
  • change the line-search algorithm with the LINESEARCH= option
  • specify a more precise line search with the LSPRECISION= option, if you use LINESEARCH=2 or LINESEARCH=3
• Change the initial values by using a grid search specification to obtain a set of good feasible starting values.

Convergence to Stationary Point

The (projected) gradient at a stationary point is zero and that results in a zero step length. The stopping criteria are satisfied.

There are two ways to avoid this situation:

• Use the DECVAR statement to specify a grid of feasible starting points.
• Use the OPTCHECK= option to avoid terminating at the stationary point.

The signs of the eigenvalues of the (reduced) Hessian matrix contain information regarding a stationary point:

• If all eigenvalues are positive, the Hessian matrix is positive definite and the point is a minimum point.
• If some of the eigenvalues are positive and all remaining eigenvalues are zero, the Hessian matrix is positive semidefinite and the point is a minimum or saddle point.
• If all eigenvalues are negative, the Hessian matrix is negative definite and the point is a maximum point.
• If some of the eigenvalues are negative and all remaining eigenvalues are zero, the Hessian matrix is negative semidefinite and the point is a maximum or saddle point.
• If all eigenvalues are zero, the point can be a minimum, maximum, or saddle point.

Precision of Solution

In some applications, PROC NLP may result in parameter estimates that are not precise enough. Usually this means that the procedure terminated too early at a point too far from the optimal point. The termination criteria define the size of the termination region around the optimal point. Any point inside this region can be accepted for terminating the optimization process. The default values of the termination criteria are set to satisfy a reasonable compromise between the computational effort (computer time) and the precision of the computed estimates for the most common applications. However, there are a number of circumstances where the default values of the termination criteria specify a region that is either too large or too small. If the termination region is too large, it can contain points with low precision. In such cases, you should inspect the log or list output to find the message stating which termination criterion terminated the optimization process. In many applications, you can obtain a solution with higher precision by simply using the old parameter estimates as starting values in a subsequent run where you specify a smaller value for the termination criterion that was satisfied at the previous run.

If the termination region is too small, the optimization process may take longer to find a point inside such a region or may not even find such a point due to rounding errors in function values and derivatives. This can easily happen in applications where finite-difference approximations of derivatives are used and the GCONV and ABSGCONV termination criteria are too small to respect rounding errors in the gradient values.