| The NLP Procedure |
Testing the Gradient Specification
There are three main ways to check the correctness of derivative specifications:
- Specify the FD= or FDHESSIAN= option in the PROC NLP statement to compute finite-difference approximations of first- and second-order derivatives. In many applications, the finite-difference approximations are computed with high precision and do not differ too much from the derivatives that are computed by specified formulas.
- Specify the GRADCHECK[=DETAIL] option in
the PROC NLP
statement to compute and display a test vector
and a test matrix of the gradient values at the starting
point
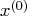 by the method of Wolfe (1982). If you do
not specify the GRADCHECK option, a fast
derivative test identical to the GRADCHECK=FAST
specification is done by default.
by the method of Wolfe (1982). If you do
not specify the GRADCHECK option, a fast
derivative test identical to the GRADCHECK=FAST
specification is done by default.
- If the default analytical derivative compiler is used or
if derivatives are specified using the GRADIENT or
JACOBIAN
statement, the gradient or Jacobian computed at the initial
point
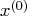 is tested by default using finite-difference
approximations. In some examples, the relative test can show
significant differences between the two forms of derivatives,
resulting in a warning message indicating that the specified
derivatives could be wrong, even if they are correct. This
happens especially in cases where the magnitude of the gradient
at the starting point
is tested by default using finite-difference
approximations. In some examples, the relative test can show
significant differences between the two forms of derivatives,
resulting in a warning message indicating that the specified
derivatives could be wrong, even if they are correct. This
happens especially in cases where the magnitude of the gradient
at the starting point 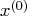 is small.
is small.
The algorithm of Wolfe (1982) is used to check whether the gradient
![]() specified by a GRADIENT statement (or
indirectly by a JACOBIAN statement) is appropriate
for the objective function
specified by a GRADIENT statement (or
indirectly by a JACOBIAN statement) is appropriate
for the objective function ![]() specified by the program statements.
specified by the program statements.
Using function and gradient evaluations in the neighborhood of
the starting point ![]() , second derivatives are approximated
by finite-difference formulas. Forward differences of gradient
values are used to approximate the Hessian element
, second derivatives are approximated
by finite-difference formulas. Forward differences of gradient
values are used to approximate the Hessian element ![]() ,
,
If the specification of the first derivatives is correct, the elements of the test vector and test matrix should be relatively small. The location of large elements in the test matrix points to erroneous coordinates in the gradient specification. For very large optimization problems, this algorithm can be too expensive in terms of computer time and memory.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.