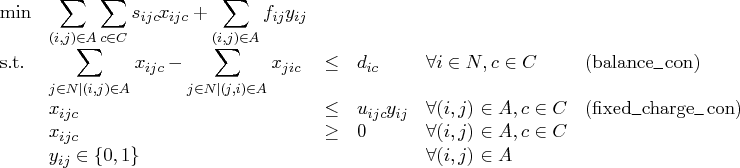| The Mixed Integer Linear Programming Solver |
Example 9.2: Multicommodity Transshipment Problem with Fixed Charges
The following application has been adapted from Example 3.14.
The following example illustrates the use of PROC OPTMODEL to generate
a mixed integer linear
program to solve a multicommodity network flow model with fixed charges.
Consider a network with nodes 
, arcs 
, and a set 
of
commodities to be shipped between the nodes.
There is a variable shipping cost 
for each of the four
commodities 
across each of the arcs 
. In addition, there is
a fixed charge 
for the
use of each arc . The shipping costs and fixed charges are defined in the
data set arcdata, as follows:
data arcdata;
array c c1-c4;
input from $ to $ c1 c2 c3 c4 fx;
datalines;
farm-a Chicago 20 15 17 22 100
farm-b Chicago 15 15 15 30 75
farm-c Chicago 30 30 10 10 100
farm-a StLouis 30 25 27 22 150
farm-c StLouis 10 9 11 10 75
Chicago NY 75 75 75 75 200
StLouis NY 80 80 80 80 200
;
run;
The supply (positive numbers) at each of the nodes and the
demand (negative numbers) at each of the nodes 
for each
commodity are shown in the data set
nodedata, as follows:
data nodedata;
array sd sd1-sd4;
input node $ sd1 sd2 sd3 sd4;
datalines;
farm-a 100 100 40 .
farm-b 100 200 50 50
farm-c 40 100 75 100
NY -150 -200 -50 -75
;
run;
Let 
define the flow of commodity across arc .
Let 
if arc is used, and 0 otherwise. Since the
total flow on an arc must be less than the total demand
across all nodes 
, we can define the trivial upper bound 
as
This model can be represented using the following mixed integer linear program:
Constraint (balance_con) ensures conservation of flow for both supply
and demand. Constraint (fixed_charge_con) models the fixed charge
cost by forcing if 
for any commodity 
.
The PROC OPTMODEL code follows.
proc optmodel presolver=none;
set COMMODITIES = 1..4;
set <str,str> ARCS;
set <str> NODES = (setof {<i,j> in ARCS} i)
union (setof {<i,j> in ARCS} j);
num shipping_cost {ARCS, COMMODITIES};
num fixed_charge {ARCS};
num supply_demand {NODES, COMMODITIES} init 0;
num upper_bound {ARCS, comm in COMMODITIES} init
sum {i in NODES: supply_demand[i,comm] < 0} (-supply_demand[i,comm]);
read data arcdata into ARCS=[from to] {comm in COMMODITIES}
<shipping_cost[from,to,comm] = col("c"||comm)> fixed_charge=fx;
read data nodedata nomiss into [node] {comm in COMMODITIES}
<supply_demand[node,comm] = col("sd"||comm)>;
var Flow {<i,j> in ARCS, comm in COMMODITIES} >= 0 <= upper_bound[i,j,comm];
var UseArc {ARCS} binary;
/* minimize shipping costs plus fixed charges */
min TotalCost =
sum {<i,j> in ARCS, comm in COMMODITIES}
shipping_cost[i,j,comm] * Flow[i,j,comm]
+ sum {<i,j> in ARCS} fixed_charge[i,j] * UseArc[i,j];
/* flow balance constraints: outflow - inflow <= supply_demand */
con balance_con {i in NODES, comm in COMMODITIES}:
sum {j in NODES: <i,j> in ARCS} Flow[i,j,comm]
- sum {j in NODES: <j,i> in ARCS} Flow[j,i,comm]
<= supply_demand[i,comm];
/* fixed charge constraints: if Flow > 0 for some commodity then UseArc = 1 */
con fixed_charge_con {<i,j> in ARCS, comm in COMMODITIES}:
Flow[i,j,comm] <= upper_bound[i,j,comm] * UseArc[i,j];
solve with milp;
print {<i,j> in ARCS, comm in COMMODITIES: Flow[i,j,comm] > 1.0e-5} Flow;
for {<i,j> in ARCS} UseArc[i,j] = round(UseArc[i,j].sol);
print UseArc;
quit;
The solution summary, as well as the output from the two PRINT statements, are shown in Output 9.2.1.
Output 9.2.1: Multicommodity Transshipment Problem with Fixed Charges Solution Summary
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.