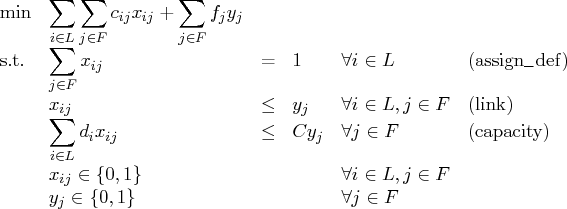| The Mixed Integer Linear Programming Solver |
Example 9.3: Facility Location
Consider the classic facility location problem. Given a set 
of customer
locations and a set 
of candidate facility sites, you must decide which sites
to build facilities on and assign coverage of customer demand to these sites so as
to minimize cost. All customer demand 
must be satisfied, and each
facility has a demand capacity limit 
. The total cost is the sum of the
distances 
between facility 
and its assigned customer 
, plus
a fixed charge 
for building a facility at site .
Let 
represent choosing
site to build a facility, and 0 otherwise. Also, let 
represent the assignment of customer to facility , and 0 otherwise.
This model can be formulated as the following integer linear program:
Constraint (assign_def) ensures that each customer is assigned to exactly one site. Constraint (link) forces a facility to be built if any customer has been assigned to that facility. Finally, constraint (capacity) enforces the capacity limit at each site.
Let us also consider a variation of this same problem where there is no cost for building a facility. This problem is typically easier to solve than the original problem. For this variant, let the objective be
First, let us construct a random instance of this problem by using the following DATA steps:
%let NumCustomers = 50;
%let NumSites = 10;
%let SiteCapacity = 35;
%let MaxDemand = 10;
%let xmax = 200;
%let ymax = 100;
%let seed = 938;
/* generate random customer locations */
data cdata(drop=i);
length name $8;
do i = 1 to &NumCustomers;
name = compress('C'||put(i,best.));
x = ranuni(&seed) * &xmax;
y = ranuni(&seed) * &ymax;
demand = ranuni(&seed) * &MaxDemand;
output;
end;
run;
/* generate random site locations and fixed charge */
data sdata(drop=i);
length name $8;
do i = 1 to &NumSites;
name = compress('SITE'||put(i,best.));
x = ranuni(&seed) * &xmax;
y = ranuni(&seed) * &ymax;
fixed_charge = 30 * (abs(&xmax/2-x) + abs(&ymax/2-y));
output;
end;
run;
In the following PROC OPTMODEL code, we first generate and solve the model with the no-fixed-charge variant of the cost function. Next, we solve the fixed-charge model. Note that the solution to the model with no fixed charge is feasible for the fixed-charge model and should provide a good starting point for the MILP solver. We use the PRIMALIN option to provide an incumbent solution (warm start).
proc optmodel;
set <str> CUSTOMERS;
set <str> SITES;
/* x and y coordinates of CUSTOMERS and SITES */
num x {CUSTOMERS union SITES};
num y {CUSTOMERS union SITES};
num demand {CUSTOMERS};
num fixed_charge {SITES};
/* distance from customer i to site j */
num dist {i in CUSTOMERS, j in SITES}
= sqrt((x[i] - x[j])^2 + (y[i] - y[j])^2);
read data cdata into CUSTOMERS=[name] x y demand;
read data sdata into SITES=[name] x y fixed_charge;
var Assign {CUSTOMERS, SITES} binary;
var Build {SITES} binary;
min CostNoFixedCharge
= sum {i in CUSTOMERS, j in SITES} dist[i,j] * Assign[i,j];
min CostFixedCharge
= CostNoFixedCharge + sum {j in SITES} fixed_charge[j] * Build[j];
/* each customer assigned to exactly one site */
con assign_def {i in CUSTOMERS}:
sum {j in SITES} Assign[i,j] = 1;
/* if customer i assigned to site j, then facility must be built at j */
con link {i in CUSTOMERS, j in SITES}:
Assign[i,j] <= Build[j];
/* each site can handle at most &SiteCapacity demand */
con capacity {j in SITES}:
sum {i in CUSTOMERS} demand[i] * Assign[i,j] <= &SiteCapacity * Build[j];
/* solve the MILP with no fixed charges */
solve obj CostNoFixedCharge with milp / printfreq = 500;
/* clean up the solution */
for {i in CUSTOMERS, j in SITES} Assign[i,j] = round(Assign[i,j]);
for {j in SITES} Build[j] = round(Build[j]);
call symput('varcostNo',put(CostNoFixedCharge,6.1));
/* create a data set for use by GPLOT */
create data CostNoFixedCharge_Data from
[customer site]={i in CUSTOMERS, j in SITES: Assign[i,j] = 1}
xi=x[i] yi=y[i] xj=x[j] yj=y[j];
/* solve the MILP, with fixed charges with warm start */
solve obj CostFixedCharge with milp / primalin printfreq = 500;
/* clean up the solution */
for {i in CUSTOMERS, j in SITES} Assign[i,j] = round(Assign[i,j]);
for {j in SITES} Build[j] = round(Build[j]);
num varcost = sum {i in CUSTOMERS, j in SITES} dist[i,j] * Assign[i,j].sol;
num fixcost = sum {j in SITES} fixed_charge[j] * Build[j].sol;
call symput('varcost', put(varcost,6.1));
call symput('fixcost', put(fixcost,5.1));
call symput('totalcost', put(CostFixedCharge,6.1));
/* create a data set for use by GPLOT */
create data CostFixedCharge_Data from
[customer site]={i in CUSTOMERS, j in SITES: Assign[i,j] = 1}
xi=x[i] yi=y[i] xj=x[j] yj=y[j];
quit;
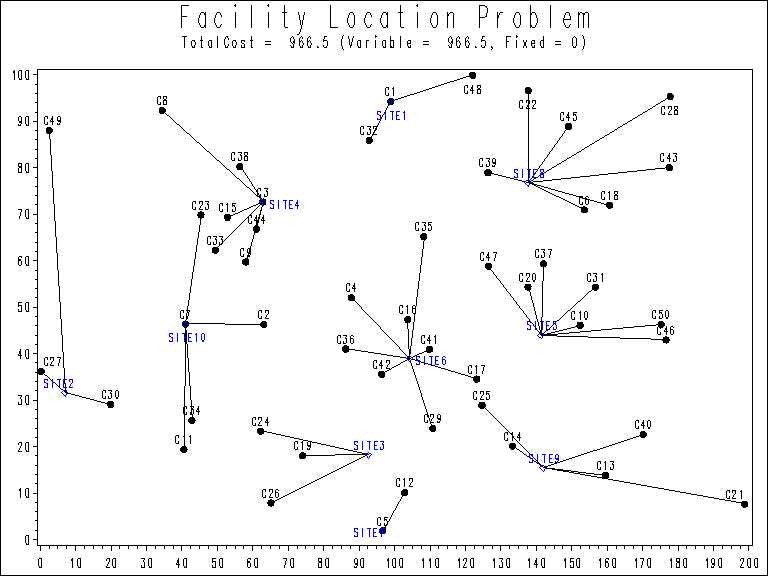
The information printed in the log for the no-fixed-charge model is displayed in Output 9.3.1.
Output 9.3.1: OPTMODEL Log for Facility Location with No Fixed ChargesThe results from the warm start approach are shown in Output 9.3.2.
Output 9.3.2: OPTMODEL Log for Facility Location with Fixed Charges, Using Warm Start
|
The following two SAS programs produce a plot of the solutions for both variants of the model, using data sets produced by PROC OPTMODEL.
title1 "Facility Location Problem";
title2 "TotalCost = &varcostNo (Variable = &varcostNo, Fixed = 0)";
data csdata;
set cdata(rename=(y=cy)) sdata(rename=(y=sy));
run;
/* create Annotate data set to draw line between customer and assigned site */
%annomac;
data anno(drop=xi yi xj yj);
%SYSTEM(2, 2, 2);
set CostNoFixedCharge_Data(keep=xi yi xj yj);
%LINE(xi, yi, xj, yj, *, 1, 1);
run;
proc gplot data=csdata anno=anno;
axis1 label=none order=(0 to &xmax by 10);
axis2 label=none order=(0 to &ymax by 10);
symbol1 value=dot interpol=none
pointlabel=("#name" nodropcollisions height=1) cv=black;
symbol2 value=diamond interpol=none
pointlabel=("#name" nodropcollisions color=blue height=1) cv=blue;
plot cy*x sy*x / overlay haxis=axis1 vaxis=axis2;
run;
quit;
The output of the first program is shown in Output 9.3.3.
Output 9.3.3: Solution Plot for Facility Location with No Fixed Charges
|
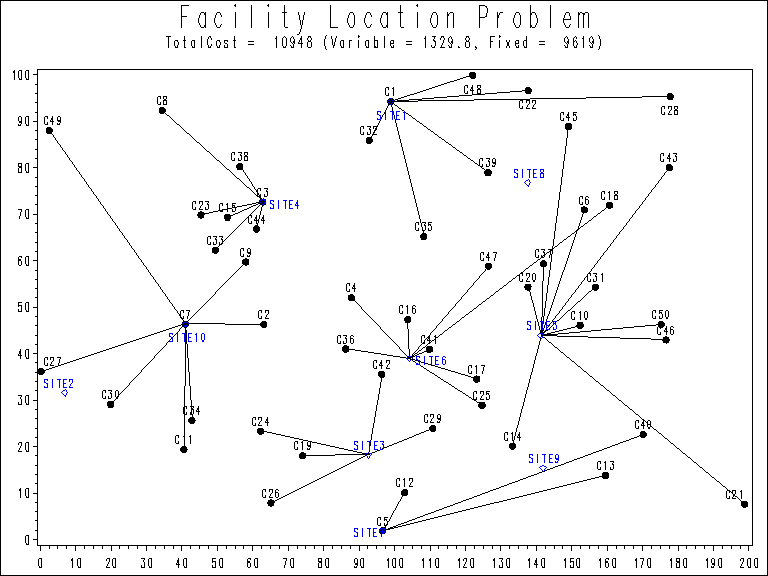
The output of the second program is shown in Output 9.3.4.
title1 "Facility Location Problem";
title2 "TotalCost = &totalcost (Variable = &varcost, Fixed = &fixcost)";
/* create Annotate data set to draw line between customer and assigned site */
data anno(drop=xi yi xj yj);
%SYSTEM(2, 2, 2);
set CostFixedCharge_Data(keep=xi yi xj yj);
%LINE(xi, yi, xj, yj, *, 1, 1);
run;
proc gplot data=csdata anno=anno;
axis1 label=none order=(0 to &xmax by 10);
axis2 label=none order=(0 to &ymax by 10);
symbol1 value=dot interpol=none
pointlabel=("#name" nodropcollisions height=1) cv=black;
symbol2 value=diamond interpol=none
pointlabel=("#name" nodropcollisions color=blue height=1) cv=blue;
plot cy*x sy*x / overlay haxis=axis1 vaxis=axis2;
run;
quit;
Output 9.3.4: Solution Plot for Facility Location with Fixed Charges
|
The economic trade-off for the fixed-charge model forces us to build fewer sites and push more demand to each site.
It is possible to expedite the solution of the fixed-charge facility location problem
by choosing appropriate branching priorities for the decision variables. Recall that
for each site , the value of the variable 
determines whether or not a facility
is built on that site. Suppose you decide to branch on the variables before the
variables 
. You can set a higher branching priority for by using the
.priority suffix for the Build variables in PROC OPTMODEL, as follows:
for{j in SITES} Build[j].priority=10;
Setting higher branching priorities for certain variables is not guaranteed to speed
up the MILP solver, but it can be helpful in some instances. The following program
creates and solves an instance of the facility location problem in which giving higher
priority to causes the MILP solver to find the optimal solution more quickly.
We use the PRINTFREQ= option to abbreviate the node log.
%let NumCustomers = 45;
%let NumSites = 8;
%let SiteCapacity = 35;
%let MaxDemand = 10;
%let xmax = 200;
%let ymax = 100;
%let seed = 2345;
/* generate random customer locations */
data cdata(drop=i);
length name $8;
do i = 1 to &NumCustomers;
name = compress('C'||put(i,best.));
x = ranuni(&seed) * &xmax;
y = ranuni(&seed) * &ymax;
demand = ranuni(&seed) * &MaxDemand;
output;
end;
run;
/* generate random site locations and fixed charge */
data sdata(drop=i);
length name $8;
do i = 1 to &NumSites;
name = compress('SITE'||put(i,best.));
x = ranuni(&seed) * &xmax;
y = ranuni(&seed) * &ymax;
fixed_charge = (abs(&xmax/2-x) + abs(&ymax/2-y)) / 2;
output;
end;
run;
proc optmodel;
set <str> CUSTOMERS;
set <str> SITES;
/* x and y coordinates of CUSTOMERS and SITES */
num x {CUSTOMERS union SITES};
num y {CUSTOMERS union SITES};
num demand {CUSTOMERS};
num fixed_charge {SITES};
/* distance from customer i to site j */
num dist {i in CUSTOMERS, j in SITES}
= sqrt((x[i] - x[j])^2 + (y[i] - y[j])^2);
read data cdata into CUSTOMERS=[name] x y demand;
read data sdata into SITES=[name] x y fixed_charge;
var Assign {CUSTOMERS, SITES} binary;
var Build {SITES} binary;
min CostFixedCharge
= sum {i in CUSTOMERS, j in SITES} dist[i,j] * Assign[i,j]
+ sum {j in SITES} fixed_charge[j] * Build[j];
/* each customer assigned to exactly one site */
con assign_def {i in CUSTOMERS}:
sum {j in SITES} Assign[i,j] = 1;
/* if customer i assigned to site j, then facility must be built at j */
con link {i in CUSTOMERS, j in SITES}:
Assign[i,j] <= Build[j];
/* each site can handle at most &SiteCapacity demand */
con capacity {j in SITES}:
sum {i in CUSTOMERS} demand[i] * Assign[i,j] <= &SiteCapacity * Build[j];
/* assign priority to Build variables (y) */
for{j in SITES} Build[j].priority=10;
/* solve the MILP with fixed charges, using branching priorities */
solve obj CostFixedCharge with milp / printfreq=1000;
quit;
The resulting output is shown in Output 9.3.5.
Output 9.3.5: PROC OPTMODEL Log for Facility Location with Branching Priorities
|
The output in Output 9.3.6 is generated by running the same program without the line that assigns higher branching priorities to the Build variables. We again use the PRINTFREQ= option to abbreviate the node log.
Output 9.3.6: PROC OPTMODEL Log for Facility Location without Branching Priorities
|
By comparing Output 9.3.5 and Output 9.3.6 you can see that in this instance, increasing the branching priorities of the Build variables results in computational savings.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.