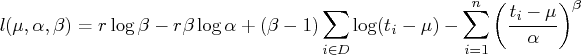The NLPC Nonlinear Optimization Solver: Example 10.2: Maximum Likelihood Weibull Model :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The NLPC Nonlinear Optimization Solver

Example 10.2: Maximum Likelihood Weibull Model

This model is obtained from Lawless (1982, pp. 190 - 194). Suppose you want to find the maximum likelihood estimates for the three-parameter Weibull model. The observed likelihood function is

$l(\mu,\alpha,\beta) = \frac{\beta^r}{\alpha^r} [ \prod_{i\in d} ( \frac{t_i - ... ...lpha} )^{\beta-1} ] \prod_{i=1}^n \exp[ -( \frac{t_i - \mu}{\alpha} )^\beta ]$

where

is the number of individuals involved in the experiment,

is the set of individuals whose lifetimes are observed, and

. Then the log-likelihood function is

$l(\mu,\alpha,\beta) = r\log\beta - r\beta\log\alpha + (\beta-1) \sum_{i \in d} \log(t_i - \mu) - \sum_{i=1}^n ( \frac{t_i - \mu}{\alpha} )^\beta$

Note that for $\beta\lt 1$ , the logarithmic terms become infinite as $\mu\!\uparrow\! \min_{i\in d}(t_i)$ . That is, $l(\mu,\alpha,\beta)$ is unbounded. Thus our interest is restricted to $\beta$ values greater than or equal to 1. Further, for the logarithmic terms to be defined, it is required that $\alpha\gt$ and $\mu\lt\min_{i\in d}(t_i)$ .

The following data from Pike (1966) represent the number of days it took the rats painted with the carcinogen DMBA to develop carcinomas:

143, 164, 188, 188, 190, 192, 206, 209, 213, 216, 220, 227,
230, 234, 246, 265, 304, 216*, 244*

Note that the last two observations have an asterisk next to them. This indicates that those two rats did not develop carcinomas. These are referred to as censored data.

For these data, a local maximum of $l(\mu,\alpha,\beta)$ occurs at $\mu^*=122$ , $\alpha^*=108.4$ , and $\beta^*=2.712$ . You can create the input data set by using the following SAS code:

    data pike;
       input days cens @@;
       datalines;
    143  0  164  0  188  0  188  0
    190  0  192  0  206  0  209  0
    213  0  216  0  220  0  227  0
    230  0  234  0  246  0  265  0
    304  0  216  1  244  1
    ;

The first observations in the data set correspond to the rats that develop carcinomas; $\min_{i\in d}(t_i)=143$ in this case. Using the preceding data, you can formulate the Weibull model as follows:

    proc optmodel;
       set S;  /* set of rats in the experiment */
       set D;  /* set of rats that develop carcinomas */
       number r = card(D);
       number t{S};
       number cens{S};
       var alpha >= 0 init 1;
       var beta  >= 1 init 1;
       var mu >= 0 <= min{i in D} t[i] init 10;
       max logl = r*log(beta) - r*beta*log(alpha)
                    + (beta - 1)*sum{i in D} log(t[i] - mu)
                    - sum{i in S} ((t[i] - mu)/alpha)^beta;
 
       read data pike into S=[_n_] t=days cens;
       D = {i in S : cens[i] = 0};
 
       solve with nlpc / printfreq=1;
       print mu alpha beta;
    quit;

Assume a starting point at $\alpha^0=1$ , $\beta^0=1$ , and $\mu^0=10$ . The data for all the rats in the experiment are read using the READ statement. The following statement subsets to the set of rats that develop carcinomas:

  
       D = {i in S : cens[i] = 0};

The NLPC solver invokes the default optimization technique (the trust region method) to solve this problem.

Figure 10.2.1 through Figure 10.2.3 show the problem summary, iteration log, solution summary, and solution. As you can see, the solution obtained by the trust region method matches closely with the local maximum given in Lawless (1982, p. 193).

Output 10.2.1: Maximum Likelihood Weibull Model: Problem Summary

Problem Summary
Objective Sense	Maximization
Objective Function	logl
Objective Type	Nonlinear

Number of Variables	3
Bounded Above	0
Bounded Below	2
Bounded Below and Above	1
Free	0
Fixed	0

Number of Constraints	0

Output 10.2.2: Maximum Likelihood Weibull Model: Iteration Log

Iteration Log: Trust Region Method
Iter	Function Calls	Objective Value	Optimality Error	Trust Region Radius
0	0	-3905	0.1874	.
1	1	-2606	0.1357	1.000
2	2	-1747	0.0990	1.015
3	3	-1235	0.0754	0.954
4	4	-959.2572	0.0620	2.060
5	5	-670.6203	0.0472	1.910
6	6	-520.6900	0.0390	3.942
7	7	-371.3259	0.0305	3.850
8	8	-292.0677	0.0256	3.987
9	9	-219.7420	0.0214	7.985
10	10	-179.8333	0.0192	8.222
11	12	-144.7603	0.0196	18.466
12	13	-125.6711	0.0248	19.148
13	17	-106.4779	1.0000	11.525
14	21	-88.1397	1.0000	15.904
15	22	-87.4005	0.4041	15.904
16	23	-87.3426	0.0115	4.288
17	24	-87.3270	0.006032	4.355
18	25	-87.3243	0.002287	4.355
19	26	-87.3242	0.0000486	2.666
20	27	-87.3242	1.4815E-8	0.359

Note:

Optimality criteria (ABSOPTTOL=0.001, RELOPTTOL=1E-6) are satisfied.

Output 10.2.3: Maximum Likelihood Weibull Model: Solution

Solution Summary
Solver	NLPC/Trust Region
Objective Function	logl
Solution Status	Optimal
Objective Value	-87.32424712
Iterations	20

Absolute Optimality Error	1.4815488E-8
Relative Optimality Error	1.4815488E-8
Absolute Infeasibility	0
Relative Infeasibility	0

mu	alpha	beta
122.03	108.38	2.7115

Top of Page