The CLP Procedure

Example 3.4 A Nonlinear Optimization Problem

This example illustrates how you can use the element constraint to represent almost any function between two variables in addition to representing nonstandard domains. Consider the following nonlinear optimization problem:

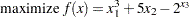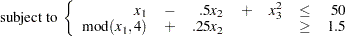You can use the CLP procedure to solve this problem by introducing four artificial variables – 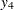to represent each of the nonlinear terms. Let 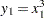, , 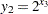, 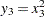and 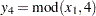. Since the domains of 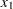and 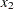are not consecutive integers that start from 1, you can use element constraints to represent their domains by using index variables 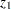and 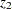, respectively. For example, either of the following two ELEMENT constraints specifies that the domain of 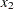is the set of odd integers in :

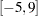element(z2,(-5,-3,-1,1,3,5,7,9),x2)
element(z2,(-5 to 9 by 2),x2) 

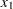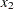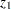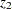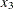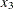Any functional dependencies on or can now be defined using or , respectively, as the index variable in an element constraint. Since the domain of is , you can directly use as the index variable in an element constraint to define dependencies on .

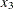For example, the following constraint specifies the function ,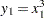

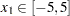
element(z1,(-125,-64,-27,-8,-1,0,1,8,27,64,125),y1)

You can solve the problem in one of the following two ways. The first way is to follow the approach of Example 3.3 by expressing the objective function as a linear constraint 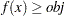. Then, you can create a SAS macro %CALLCLP with parameter obj and call it iteratively to determine the optimal value of the objective function.

The second way is to define the objective function in the Constraint data set, as demonstrated in the following statements. The data set objdata specifies that the objective function 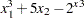is to be maximized.

data objdata;      
   input y1 x2 y2 _TYPE_ $ _RHS_;
/* Objective function: x1^3 + 5 * x2 - 2^x3 */
   datalines;
1 5 -1 MAX .
;

proc clp condata=objdata out=clpout;
   var x1=[-5, 5] x2=[-5, 9] x3=[1, 10] (y1-y4) (z1-z2);

   /* Use element constraint to represent non-contiguous domains */
   /* and nonlinear functions.                                   */
   element 

      /* Domain of x1 is [-5,5] */
      (z1, ( -5 to 5), x1)

      /* Functional Dependencies on x1 */ 
      /* y1 = x1^3 */  
      (z1, (-125, -64, -27, -8, -1, 0, 1, 8, 27, 64, 125), y1)
      /* y4 = mod(x1, 4) */
      (z1, ( -1,  0,  -3,  -2,  -1, 0, 1, 2, 3, 0, 1), y4)

      /* Domain of x2 is the set of odd numbers in [-5, 9] */
      (z2, (-5 to 9 by 2), x2)

      /* Functional Dependencies on x3 */ 
      /* y2 = 2^x3 */
      (x3, (2, 4, 8, 16, 32, 64, 128, 256, 512, 1024), y2)
      /* y3 = x3^2 */
      (x3, (1, 4, 9, 16, 25, 36, 49, 64, 81, 100), y3);

   lincon 
      /* x1 - .5 * x2 + x3^2 <=50 */
      x1 - .5 * x2 + y3 <= 50,

      /* mod(x1, 4) + .25 * x2 >= 1.5 */
      y4 + .25 * x2 >= 1.5;
run;
%put &_ORCLP_;
proc print data=clpout; run;

Output 3.4.1 shows the solution that corresponds to the optimal objective value of 168.