The CLP Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details

-
Examples
 Logic-Based Puzzles Alphabet Blocks Problem Work-Shift Scheduling Problem A Nonlinear Optimization Problem Car Painting Problem Scene Allocation Problem Car Sequencing Problem Round-Robin Problem Resource-Constrained Scheduling with Nonstandard Temporal Constraints Scheduling with Alternate Resources 10×10 Job Shop Scheduling Problem Scheduling a Major Basketball Conference Statement and Option Cross-Reference Table
Logic-Based Puzzles Alphabet Blocks Problem Work-Shift Scheduling Problem A Nonlinear Optimization Problem Car Painting Problem Scene Allocation Problem Car Sequencing Problem Round-Robin Problem Resource-Constrained Scheduling with Nonstandard Temporal Constraints Scheduling with Alternate Resources 10×10 Job Shop Scheduling Problem Scheduling a Major Basketball Conference Statement and Option Cross-Reference Table - References
Example 3.3 Work-Shift Scheduling Problem
This example illustrates the use of the GCC constraint in finding a feasible solution to a work-shift scheduling problem and then using the element constraint to incorporate cost information in order to find a minimum cost schedule.
Six workers (Alan, Bob, John, Mike, Scott, and Ted) are to be assigned to three working shifts. The first shift needs at least one and at most four people; the second shift needs at least two and at most three people; and the third shift needs exactly two people. Alan does not work on the first shift; Bob works only on the third shift. The others can work any shift. The objective is to find a feasible assignment for this problem.
You can model the minimum and maximum shift requirements with a GCC constraint and formulate the problem as a standard CSP. The variables W1–W6 identify the shift to be assigned to each of the six workers: Alan, Bob, John, Mike, Scott, and Ted.
proc clp out=clpout;
/* Six workers (Alan, Bob, John, Mike, Scott and Ted)
are to be assigned to 3 working shifts. */
var (W1-W6) = [1,3];
/* The first shift needs at least 1 and at most 4 people;
the second shift needs at least 2 and at most 3 people;
and the third shift needs exactly 2 people. */
gcc (W1-W6) = ( ( 1, 1, 4) ( 2, 2, 3) ( 3, 2, 2) );
/* Alan doesn't work on the first shift. */
lincon W1 <> 1;
/* Bob works only on the third shift. */
lincon W2 = 3;
run;
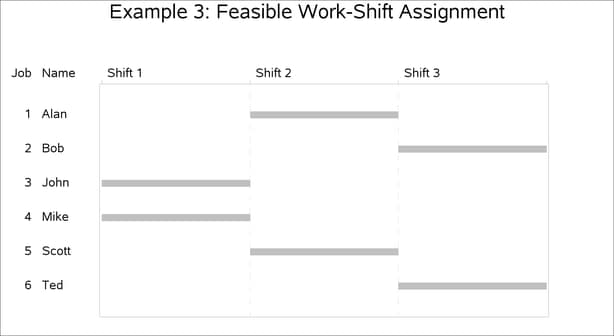
The resulting assignment is shown in Output 3.3.1.
| Solution to Work-Shift Scheduling Problem |
| Obs | W1 | W2 | W3 | W4 | W5 | W6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 1 | 2 | 3 |
A Gantt chart of the corresponding schedule is displayed in Output 3.3.2.
Now suppose that every work-shift assignment has a cost associated with it and that the objective of interest is to determine the schedule with minimum cost.
The costs of assigning the workers to the different shifts are given in Table 3.8. A dash "-" in position  indicates that worker
indicates that worker 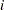 cannot work on shift
cannot work on shift 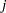 .
.
Shift 1 |
Shift 2 |
Shift 3 |
|
Alan |
- |
12 |
10 |
Bob |
- |
- |
6 |
John |
16 |
8 |
12 |
Mike |
10 |
6 |
8 |
Scott |
6 |
6 |
8 |
Ted |
12 |
4 |
4 |
Based on the cost structure in Table 3.8, the schedule derived previously has a cost of 54. The objective now is to determine the optimal schedule—one that results in the minimum cost.
Let the variable 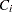 represent the cost of assigning worker
represent the cost of assigning worker 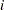 to a shift. This variable is shift-dependent and is given a high value (for example, 100) if the worker cannot be assigned to a shift. The costs can also be interpreted as preferences if desired. You can use an element constraint to associate the cost
to a shift. This variable is shift-dependent and is given a high value (for example, 100) if the worker cannot be assigned to a shift. The costs can also be interpreted as preferences if desired. You can use an element constraint to associate the cost 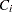 with the shift assignment for each worker. For example,
with the shift assignment for each worker. For example, 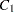 , the cost of assigning Alan to a shift, can be determined by the constraint ELEMENT(
, the cost of assigning Alan to a shift, can be determined by the constraint ELEMENT( ).
).
By adding a linear constraint 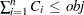 , you can limit the solutions to feasible schedules that cost no more than obj.
, you can limit the solutions to feasible schedules that cost no more than obj.
You can then create a SAS macro %CALLCLP with obj as a parameter that can be called iteratively from a search routine to find an optimal solution. The SAS macro %MINCOST(lb,ub) uses a bisection search to find the minimum cost schedule among all schedules that cost between lb and ub. Although a value of ub 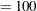 is used in this example, it would suffice to use ub
is used in this example, it would suffice to use ub  , the cost of the feasible schedule determined earlier.
, the cost of the feasible schedule determined earlier.
%macro callclp(obj);
%put The objective value is: &obj..;
proc clp out=clpout;
/* Six workers (Alan, Bob, John, Mike, Scott and Ted)
are to be assigned to 3 working shifts. */
var (W1-W6) = [1,3];
var (C1-C6) = [1,100];
/* The first shift needs at least 1 and at most 4 people;
the second shift needs at least 2 and at most 3 people;
and the third shift needs exactly 2 people. */
gcc (W1-W6) = ( ( 1, 1, 4) ( 2, 2, 3) ( 3, 2, 2) );
/* Alan doesn't work on the first shift. */
lincon W1 <> 1;
/* Bob works only on the third shift. */
lincon W2 = 3;
/* Specify the costs of assigning the workers to the shifts.
Use 100 (a large number) to indicate an assignment
that is not possible.*/
element (W1, (100, 12, 10), C1);
element (W2, (100, 100, 6), C2);
element (W3, ( 16, 8, 12), C3);
element (W4, ( 10, 6, 8), C4);
element (W5, ( 6, 6, 8), C5);
element (W6, ( 12, 4, 4), C6);
/* The total cost should be no more than the given objective value. */
lincon C1 + C2 + C3 + C4 + C5 + C6 <= &obj;
run;
/* when a solution is found, */
/* &_ORCLP_ contains the string SOLUTIONS_FOUND */
%if %index(&_ORCLP_, SOLUTIONS_FOUND) %then %let clpreturn=SUCCESSFUL;
%mend;
/* Bisection search method to determine the optimal objective value */
%macro mincost(lb, ub);
%do %while (&lb<&ub-1);
%put Currently lb=&lb, ub=&ub..;
%let newobj=%eval((&lb+&ub)/2);
%let clpreturn=NOTFOUND;
%callclp(&newobj);
%if &clpreturn=SUCCESSFUL %then %let ub=&newobj;
%else %let lb=&newobj;
%end;
%callclp(&ub);
%put Minimum possible objective value within given range is &ub.;
%put Any value less than &ub makes the problem infeasible. ;
proc print;
run;
%mend;
/* Find the minimum objective value between 1 and 100. */
%mincost(lb=1, ub=100);
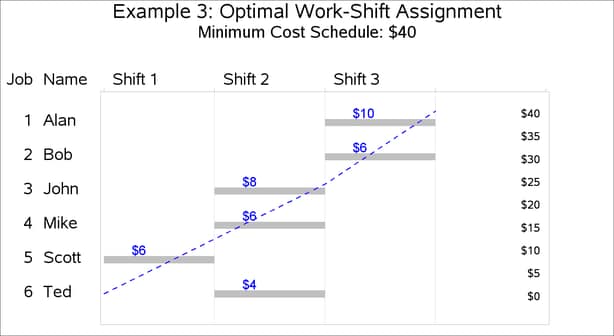
The cost of the optimal schedule, which corresponds to the solution shown in the following output, is 40.
| Solution to Optimal Work-Shift Scheduling Problem |
| Obs | W1 | W2 | W3 | W4 | W5 | W6 | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 3 | 2 | 2 | 1 | 2 | 10 | 6 | 8 | 6 | 6 | 4 |
The minimum cost schedule is displayed in the Gantt chart in Output 3.3.3.