PROC CLP: The CLP Procedure :: SAS/OR(R) 9.2 User's Guide: Constraint Programming

The CLP Procedure

The CLP procedure is a finite-domain constraint programming solver for CSPs. In the context of the CLP procedure, CSPs can be classified into two types: standard CSPs and scheduling CSPs. A standard CSP is characterized by integer variables, linear constraints, array-type constraints, global constraints, and reified constraints. In other words, 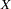$\text{[math]}$ is a finite set of integer variables, and $\text{[math]}$ can contain linear, array, global, or logical constraints. A scheduling CSP is characterized by activities, temporal constraints, and resource requirement constraints. 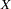In other words, $\text{[math]}$ is a finite set of activities, and $\text{[math]}$ is a set of temporal constraints and resource requirement constraints. The CSP type is determined by the presence of either the OUT= option or the SCHEDDATA= option in the PROC CLP statement.

Specifying the OUT= option in the PROC CLP statement indicates to the CLP procedure that the CSP is a standard type. As such, the procedure will expect VAR, LINCON, REIFY, ALLDIFF, ARRAY, and FOREACH statements. You can also specify a Constraint data set by using the CONDATA= option in the PROC CLP statement in lieu of, or in combination with, VAR and LINCON statements.

Specifying the SCHEDDATA= option in the PROC CLP statement indicates to the CLP procedure that the CSP is a scheduling type. As such, the procedure will expect ACTIVITY, RESOURCE, REQUIRES, and SCHEDULE statements. You can also specify an Activity data set by using the ACTDATA= option in the PROC CLP statement in lieu of, or in combination with, the ACTIVITY statement. Precedence relationships between activities must be defined using the ACTDATA= data set. Resource requirements of activities must be defined using the RESOURCE and REQUIRES statements.

The output data set contains any solutions determined by the CLP procedure. For more information about the format and layout, see the section Details: CLP Procedure.

Consistency Techniques

The CLP procedure features a full look-ahead algorithm for standard CSPs that follows a strategy of maintaining a version of generalized arc consistency that is based on the AC-3 consistency routine (Mackworth; 1977). This strategy maintains consistency between the selected variables and the unassigned variables and also maintains consistency between unassigned variables. For the scheduling CSPs, the CLP procedure uses a forward checking algorithm, an arc-consistency routine for maintaining consistency between unassigned activities, and energetic-based reasoning methods for resource-constrained scheduling that feature the edge-finder algorithm (Applegate and Cook; 1991). You can elect to turn off some of these consistency techniques in the interest of performance.

Selection Strategy

A search algorithm for CSPs searches systematically through the possible assignments of values to variables. The order in which a variable is selected can be based on a static ordering, which is determined before the search begins, or on a dynamic ordering, in which the choice of the next variable depends on the current state of the search. The VARSELECT= option in the PROC CLP statement defines the variable selection strategy for a standard CSP. The default strategy is the dynamic MINR strategy, which selects the variable with the smallest range. The ACTSELECT= option in the SCHEDULE statement defines the activity selection strategy for a scheduling CSP. The default strategy is the RAND strategy, which selects an activity at random from the set of activities that begin prior to the earliest early finish time. This strategy was proposed by Nuijten (1994).

Assignment Strategy

Once a variable or an activity has been selected, the assignment strategy dictates the value that is assigned to it. For variables, the assignment strategy is specified with the VARASSIGN= option in the PROC CLP statement. The default assignment strategy selects the minimum value from the domain of the selected variable. For activities, the assignment strategy is specified with the ACTASSIGN= option in the SCHEDULE statement. The default strategy of RAND assigns the time to the earliest start time, and the resources are chosen randomly from the set of resource assignments that support the selected start time.

Note: This procedure is experimental.

Top of Page