REIFY variable : (linear_constraint) <...> ;

linear_term_1 operator linear_term_2

where a linear_term is of the form

((<+|-> variable | number <* variable >)...)

The keyword operator can be one of the following:

<, <=, =, >=, >, <>, LE, EQ, GE, LT, GT, NE

The REIFY statement associates a binary variable with a linear constraint. The value of the binary variable is 1 or 0 depending on whether the linear constraint is satisfied or not, respectively. The linear constraint is said to be reified, and the binary variable is referred to as the control variable. As with the other variables, the control variable must also be defined in a VAR statement or in the CONDATA= data set.

The REIFY statement provides a convenient mechanism for expressing logical constraints, such as disjunctive and implicative constraints. For example, the disjunctive constraint

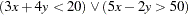can be expressed with the following statements:

   var x y p q;
   reify p: (3 * x + 4 * y < 20) q: (5 * x - 2 * y > 50);
   lincon p + q >= 1;

The binary variables and reify the linear constraints

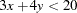and

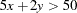respectively. The following linear constraint enforces the desired disjunction:

The REIFY constraint can also be used to express a constraint involving the absolute value of a variable. For example, the constraint

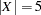can be expressed with the following statements:

   var x p q;
   reify p: (x = 5) q: (x = -5);
   lincon p + q = 1;