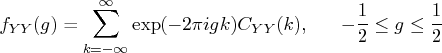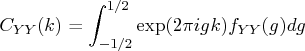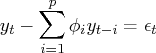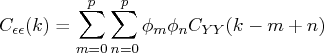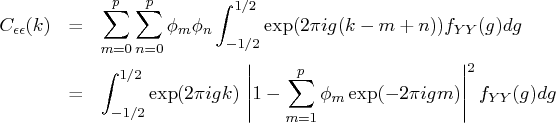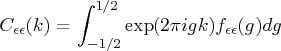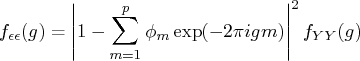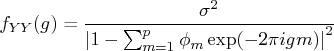| Time Series Analysis and Examples |
The autocovariance function of the
random variable 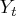 is defined as
is defined as
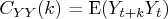
where
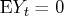
.
When the real valued process
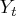
is stationary
and its autocovariance is absolutely summable, the
population spectral density function is obtained by using
the Fourier transform of the autocovariance function
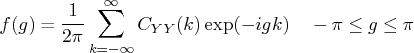
where
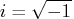
and
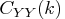
is the
autocovariance function such that
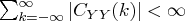
.
Consider the autocovariance generating function
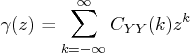
where
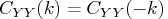
and
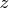
is a complex scalar.
The spectral density function can be represented as
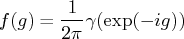
The stationary ARMA(
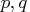
) process is denoted
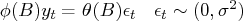
where
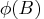
and
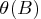
do not have common roots.
Note that the autocovariance generating function of the
linear process
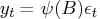
is given by
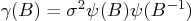
For the ARMA(
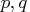
) process,
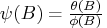
.
Therefore, the spectral density function of the stationary ARMA(
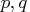
)
process becomes
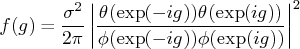
The spectral density function of a white noise is a constant.
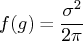
The spectral density function of the AR(1) process
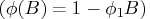
is given by
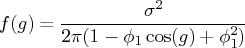
The spectrum of the AR(1) process has its minimum at
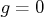
and its maximum at
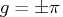
if
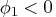
, while the spectral
density function attains its maximum at
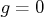
and its minimum at
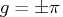
, if
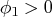
. When the series is positively
autocorrelated, its spectral density function is dominated by low
frequencies. It is interesting to observe that the spectrum approaches
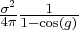
as
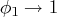
.
This relationship shows that the series is difference-stationary if
its spectral density function has a remarkable peak near 0.
The spectrum of AR(2) process 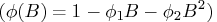 equals
equals
![f(g) = \frac{\sigma^2}{2\pi}\frac{1} {\{-4\phi_2[\cos(g)+\frac{\phi_1(1-\phi_2)} {4\phi_2}]^2 + \frac{(1+\phi_2)^2(4\phi_2 + \phi_1^2)} {4\phi_2}\}}](images/timeseriesexpls_timeseriesexplseq260.gif)
Refer to Anderson (1971) for details of the characteristics of
this spectral density function of the AR(2) process.
In practice, the population spectral density function cannot
be computed. There are many ways of computing the sample
spectral density function.
The TSBAYSEA and TSMLOCAR subroutines compute the power spectrum
by using AR coefficients and the white noise variance.
The power spectral density function of 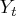 is derived by using the
Fourier transformation of
is derived by using the
Fourier transformation of 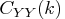 .
.
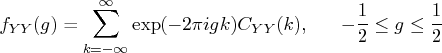
where
and
denotes frequency.
The autocovariance function can also be written as
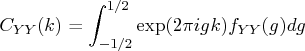
Consider the following stationary AR(
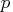
) process:
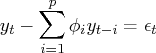
where
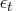
is a white noise with mean zero and
constant variance
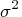
.
The autocovariance function of white noise
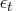 equals
equals
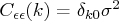
where
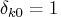
if
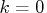
;
otherwise,
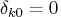
. Therefore, the power spectral
density of the white noise is
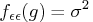
,
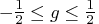
. Note that, with
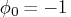
,
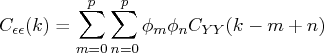
Using the following autocovariance function of
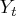
,
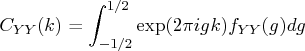
the autocovariance function of the white noise is denoted as
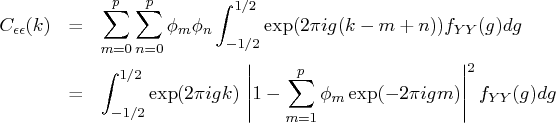
On the other hand, another formula of the
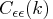
gives
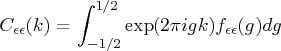
Therefore,
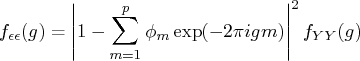
Since
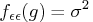
,
the rational spectrum of
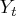
is
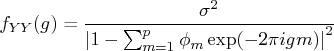
To compute the power spectrum, estimated values of white noise variance
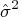
and AR coefficients
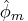
are used. The order of the AR process can be determined by using
the minimum AIC procedure.
![]() is defined as
is defined as
![]() equals
equals
![]() is derived by using the
Fourier transformation of
is derived by using the
Fourier transformation of ![]() .
.
![]() equals
equals
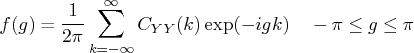
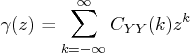
![f(g) = \frac{\sigma^2}{2\pi}\frac{1} {\{-4\phi_2[\cos(g)+\frac{\phi_1(1-\phi_2)} {4\phi_2}]^2 + \frac{(1+\phi_2)^2(4\phi_2 + \phi_1^2)} {4\phi_2}\}}](images/timeseriesexpls_timeseriesexplseq260.gif)