| Time Series Analysis and Examples |
Consider the univariate AR(
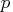
) process
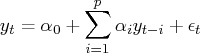
Define the design matrix
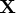
.
![{x}= [1 & y_p & ... & y_1 \ \vdots & \vdots & \ddots & \vdots \ 1 & y_{t-1} & ... & y_{t-p} ]](images/timeseriesexpls_timeseriesexplseq282.gif)
Let
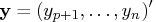
.
The least squares estimate,
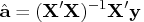
,
is the approximation to the maximum likelihood
estimate of
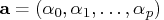
if
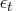
is assumed to be Gaussian
error disturbances. Combining
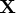
and
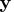
as
![{z}= [{x}\,\vdots\,{y}]](images/timeseriesexpls_timeseriesexplseq286.gif)
the
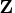
matrix can be decomposed as
![{z}= {q}{u}= {q}[{{r}}& {w}_1 \ 0 & {w}_2 ]](images/timeseriesexpls_timeseriesexplseq288.gif)
where
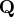
is an orthogonal matrix and
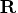
is an upper
triangular matrix,
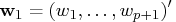
, and
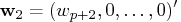
.
![{q}^'{y}= [w_1 \ w_2 \ \vdots \ w_{t-p} ]](images/timeseriesexpls_timeseriesexplseq293.gif)
The least squares estimate that uses Householder transformation
is computed by solving the linear system
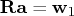
The unbiased residual variance estimate is
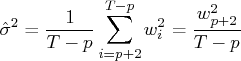
and
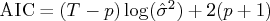
In practice, least squares estimation does not require the
orthogonal matrix
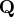
. The TIMSAC subroutines compute
the upper triangular matrix without computing the matrix
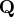
.
Consider the additive time series model
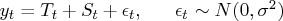
Practically, it is not possible to estimate parameters
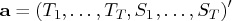 , since the number of
parameters exceeds the number of available observations.
Let
, since the number of
parameters exceeds the number of available observations.
Let 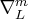 denote the seasonal difference operator with
denote the seasonal difference operator with 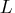 seasons and degree of
seasons and degree of 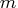 ; that is,
; that is, 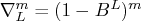 .
Suppose that
.
Suppose that 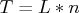 . Some constraints on the trend and seasonal
components need to be imposed such that the sum of squares of
. Some constraints on the trend and seasonal
components need to be imposed such that the sum of squares of
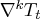 ,
, 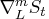 , and
, and 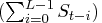 is
small. The constrained least squares estimates are obtained by
minimizing
is
small. The constrained least squares estimates are obtained by
minimizing
![\sum_{t=1}^t \{(y_t-t_t-s_t)^2 + d^2[s^2(\nabla^k t_t)^2 + (\nabla_l^m s_t)^2 + z^2(s_t+ ... +s_{t-l+1})^2]\}](images/timeseriesexpls_timeseriesexplseq305.gif)
Using matrix notation,
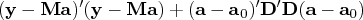
where
![{m}= [{i}_t\,\vdots\,{i}_t]](images/timeseriesexpls_timeseriesexplseq307.gif)
,
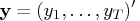
,
and
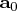
is the initial guess of
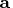
. The matrix
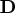
is a
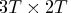
control matrix in which structure varies
according to the order of differencing in trend and season.
![{d}= d [{e}_m & 0 \ z{f}& 0 \ 0 & s{g}_k ]](images/timeseriesexpls_timeseriesexplseq311.gif)
where
![{e}_m & = & {c}_m\otimes{i}_l,\hspace*{.25in} m=1,2,3 \ {f}& = & [1 & 0 & ...... ...s & \ddots & \ddots & \ddots & 0 \ 0 & ... & 0 & -1 & 3 & -3 & 1 ]_{tx t}](images/timeseriesexpls_timeseriesexplseq312.gif)
The
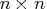
matrix
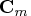
has the same structure
as the matrix
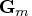
, and
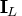
is the
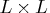
identity matrix.
The solution of the constrained least squares method is equivalent
to that of maximizing the function
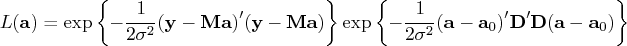
Therefore, the PDF of the data
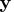
is
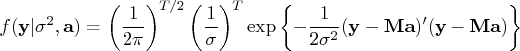
The prior PDF of the parameter vector
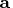
is
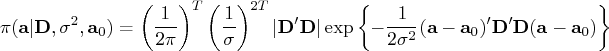
When the constant
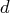
is known, the estimate
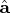
of
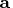
is the mean of the posterior distribution, where
the posterior PDF of the parameter
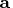
is proportional to
the function
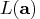
.
It is obvious that
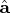
is the minimizer of
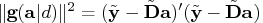
,
where
![\tilde{{y}} = [{y}\ {d}{a}_0 ]](images/timeseriesexpls_timeseriesexplseq324.gif)
![\tilde{{d}} = [{m}\ {d} ]](images/timeseriesexpls_timeseriesexplseq325.gif)
The value of
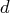
is determined by the minimum ABIC
procedure. The ABIC is defined as
![{\rm abic} = t\log[\frac{1}t\vert{g}({a}| d)\vert^2] + 2\{\log[\det({d}^'{d}+{m}^'{m})] - \log[\det({d}^'{d})]\}](images/timeseriesexpls_timeseriesexplseq326.gif)
In this section, the mathematical formulas for state space
modeling are introduced. The Kalman filter algorithms are
derived from the state space model. As an example, the state
space model of the TSDECOMP subroutine is formulated.
Define the following state space model:
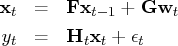
where
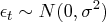
and
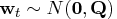
.
If the observations,
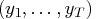
, and the initial
conditions,
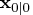
and
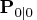
, are
available, the one-step predictor
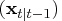
of the state vector
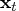
and its mean square error (MSE)
matrix
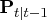
are
written as
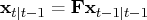
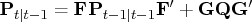
Using the current observation, the filtered value of
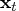
and its variance
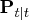
are updated.
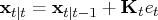
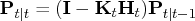
where
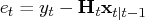
and
![{k}_t = {p}_{t| t-1}{h}^'_t[{h}_t {p}_{t| t-1}{h}^'_t + \sigma^2{i}]^{-1}](images/timeseriesexpls_timeseriesexplseq342.gif)
.
The log-likelihood function is computed as
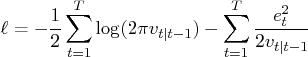
where
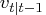
is the conditional variance of
the one-step prediction error
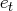
.
Consider the additive time series decomposition
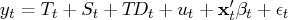
where
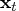
is a
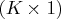
regressor vector and
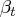
is a
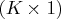
time-varying coefficient vector.
Each component has the following constraints:
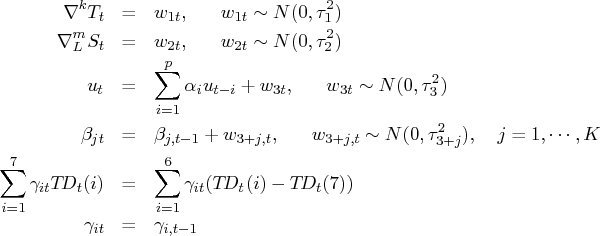
where
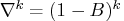
and
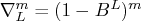
.
The AR component
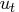
is assumed to be stationary. The
trading-day component
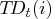
represents the number of the
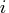
th day of the week in time
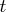
.
If
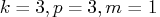
, and
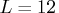
(monthly data),
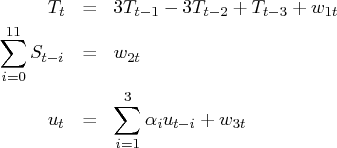
The state vector is defined as
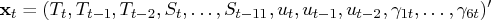
The matrix
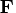
is
![{f}= [{f}_1 & 0 & 0 & 0 \ 0 & {f}_2 & 0 & 0 \ 0 & 0 & {f}_3 & 0 \ 0 & 0 & 0 & {f}_4 ]](images/timeseriesexpls_timeseriesexplseq357.gif)
where
![{f}_1 = [3 & -3 & \phantom{-}1 \ 1 & 0 & 0 \ 0 & 1 & 0 ]](images/timeseriesexpls_timeseriesexplseq358.gif)
![{f}_2 = [-1^' & -1 \ {i}_{10} & 0 ]](images/timeseriesexpls_timeseriesexplseq359.gif)
![{f}_3 = [\alpha_1 & \alpha_2 & \alpha_3 \ 1 & 0 & 0 \ 0 & 1 & 0 ]](images/timeseriesexpls_timeseriesexplseq360.gif)
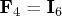
The matrix  can be denoted as
can be denoted as
![g = [{g}_1 & 0 & 0 \ 0 & {g}_2 & 0 \ 0 & 0 & {g}_3 \ 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 ]](images/timeseriesexpls_timeseriesexplseq364.gif)
where
![{g}_1 = {g}_3 = [1 & 0 & 0 ]^'](images/timeseriesexpls_timeseriesexplseq365.gif)
![{g}_2 = [1 & 0 & 0 & 0 & 0 & 0 ]^'](images/timeseriesexpls_timeseriesexplseq366.gif)
Finally, the matrix
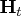
is time-varying,
![{h}_t = [1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & {h}^'_t ]](images/timeseriesexpls_timeseriesexplseq368.gif)
where
![{h}_t & = & [d_t(1) & d_t(2) & d_t(3) & d_t(4) & d_t(5) & d_t(6) ]^' \ d_t(i) & = & t\!d_t(i)-t\!d_t(7),\hspace*{.5in}i=1, ... ,6](images/timeseriesexpls_timeseriesexplseq369.gif)
![]() , since the number of
parameters exceeds the number of available observations.
Let
, since the number of
parameters exceeds the number of available observations.
Let ![]() denote the seasonal difference operator with
denote the seasonal difference operator with ![]() seasons and degree of
seasons and degree of ![]() ; that is,
; that is, ![]() .
Suppose that
.
Suppose that ![]() . Some constraints on the trend and seasonal
components need to be imposed such that the sum of squares of
. Some constraints on the trend and seasonal
components need to be imposed such that the sum of squares of
![]() ,
, ![]() , and
, and ![]() is
small. The constrained least squares estimates are obtained by
minimizing
is
small. The constrained least squares estimates are obtained by
minimizing
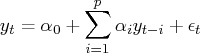
![{x}= [1 & y_p & ... & y_1 \ \vdots & \vdots & \ddots & \vdots \ 1 & y_{t-1} & ... & y_{t-p} ]](images/timeseriesexpls_timeseriesexplseq282.gif)
![{q}^'{y}= [w_1 \ w_2 \ \vdots \ w_{t-p} ]](images/timeseriesexpls_timeseriesexplseq293.gif)
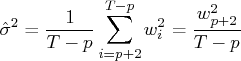
![\sum_{t=1}^t \{(y_t-t_t-s_t)^2 + d^2[s^2(\nabla^k t_t)^2 + (\nabla_l^m s_t)^2 + z^2(s_t+ ... +s_{t-l+1})^2]\}](images/timeseriesexpls_timeseriesexplseq305.gif)
![{d}= d [{e}_m & 0 \ z{f}& 0 \ 0 & s{g}_k ]](images/timeseriesexpls_timeseriesexplseq311.gif)
![{e}_m & = & {c}_m\otimes{i}_l,\hspace*{.25in} m=1,2,3 \ {f}& = & [1 & 0 & ...... ...s & \ddots & \ddots & \ddots & 0 \ 0 & ... & 0 & -1 & 3 & -3 & 1 ]_{tx t}](images/timeseriesexpls_timeseriesexplseq312.gif)
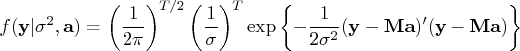
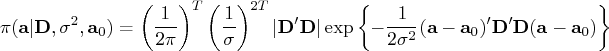
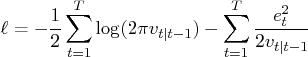
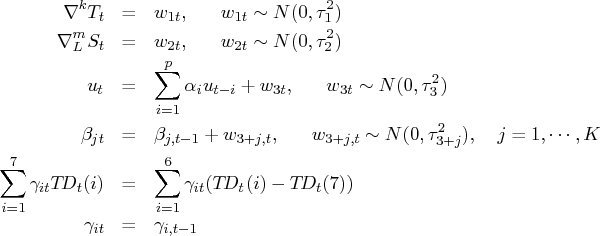
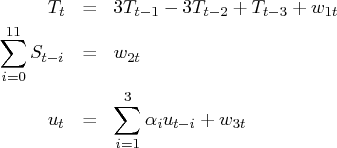
![{f}= [{f}_1 & 0 & 0 & 0 \ 0 & {f}_2 & 0 & 0 \ 0 & 0 & {f}_3 & 0 \ 0 & 0 & 0 & {f}_4 ]](images/timeseriesexpls_timeseriesexplseq357.gif)
![{f}_1 = [3 & -3 & \phantom{-}1 \ 1 & 0 & 0 \ 0 & 1 & 0 ]](images/timeseriesexpls_timeseriesexplseq358.gif)
![{f}_3 = [\alpha_1 & \alpha_2 & \alpha_3 \ 1 & 0 & 0 \ 0 & 1 & 0 ]](images/timeseriesexpls_timeseriesexplseq360.gif)
![g = [{g}_1 & 0 & 0 \ 0 & {g}_2 & 0 \ 0 & 0 & {g}_3 \ 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 ]](images/timeseriesexpls_timeseriesexplseq364.gif)
![{h}_t & = & [d_t(1) & d_t(2) & d_t(3) & d_t(4) & d_t(5) & d_t(6) ]^' \ d_t(i) & = & t\!d_t(i)-t\!d_t(7),\hspace*{.5in}i=1, ... ,6](images/timeseriesexpls_timeseriesexplseq369.gif)