| Time Series Analysis and Examples |
Consider the time series 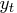 :
:
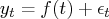
where
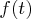
is an unknown smooth function and
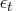
is an
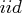
random variable with
zero mean and positive variance
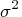
.
Whittaker (1923) provides the solution, which
balances a tradeoff between closeness to the data
and the
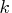
th-order difference equation.
For a fixed value of
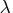
and
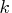
, the solution
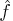
satisfies
![\min_f \sum_{t=1}^t \{ [y_t - f(t)]^2 + \lambda^2 [\nabla^k f(t)]^2 \}](images/timeseriesexpls_timeseriesexplseq110.gif)
where
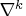
denotes the
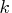
th-order difference operator.
The value of
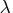
can be viewed
as the smoothness tradeoff measure.
Akaike (1980a) proposed the Bayesian
posterior PDF to solve this problem.
![\ell(f) = \exp \{ -\frac{1}{2 \sigma^2} \sum_{t=1}^t [y_t - f(t)]^2 \} \exp \{ -\frac{\lambda^2}{2 \sigma^2} \sum_{t=1}^t [\nabla^k f(t)]^2 \}](images/timeseriesexpls_timeseriesexplseq112.gif)
Therefore, the solution can be obtained
when the function
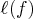
is maximized.
Assume that time series is decomposed as follows:
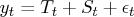
where
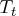
denotes the trend component
and
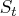
is the seasonal component.
The trend component follows the
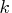
th-order
stochastically perturbed difference equation.
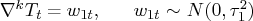
For example, the polynomial trend
component for
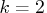
is written as

To accommodate regular seasonal effects, the
stochastic seasonal relationship is used.
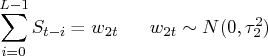
where
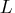
is the number of seasons within a period.
In the context of Whittaker and Akaike, the smoothness
priors problem can be solved by the maximization of
![\ell(f) & = & \exp [ -\frac{1}{2 \sigma^2} \sum_{t=1}^t (y_t - t_t - s_t)^2 ... ...\frac{\tau_2^2}{2 \sigma^2} \sum_{t=1}^t ( \sum_{i=0}^{l-1} s_{t-i} )^2 ]](images/timeseriesexpls_timeseriesexplseq119.gif)
The values of hyperparameters
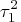
and
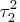
refer to a measure of uncertainty of prior information.
For example, the large value of
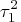
implies a relatively smooth trend component.
The ratio
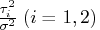
can be considered as a signal-to-noise ratio.
Kitagawa and Gersch (1984) use the Kalman filter recursive
computation for the likelihood of the tradeoff parameters.
The hyperparameters are estimated by combining
the grid search and optimization method.
The state space model and Kalman filter recursive
computation are discussed in the section "State Space and Kalman Filter Method".
![]() :
:
![\min_f \sum_{t=1}^t \{ [y_t - f(t)]^2 + \lambda^2 [\nabla^k f(t)]^2 \}](images/timeseriesexpls_timeseriesexplseq110.gif)
![\ell(f) = \exp \{ -\frac{1}{2 \sigma^2} \sum_{t=1}^t [y_t - f(t)]^2 \} \exp \{ -\frac{\lambda^2}{2 \sigma^2} \sum_{t=1}^t [\nabla^k f(t)]^2 \}](images/timeseriesexpls_timeseriesexplseq112.gif)
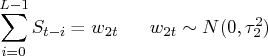
![\ell(f) & = & \exp [ -\frac{1}{2 \sigma^2} \sum_{t=1}^t (y_t - t_t - s_t)^2 ... ...\frac{\tau_2^2}{2 \sigma^2} \sum_{t=1}^t ( \sum_{i=0}^{l-1} s_{t-i} )^2 ]](images/timeseriesexpls_timeseriesexplseq119.gif)