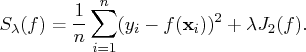| Language Reference |
TPSPLINE Call
computes thin-plate smoothing splines
- CALL TPSPLINE( fitted, coeff, adiag, gcv,
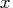 ,
, 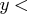 ,
lambda> );
,
lambda> );
The TSPLINE subroutine computes thin-plate smoothing spline (TPSS) fits to approximate smooth multivariate functions that are observed with noise. The generalized cross validation (GCV) function is used to select the smoothing parameter.
The TPSPLINE subroutine returns the following values:
- fitted
- is an
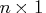 vector of fitted values of the
TPSS fit evaluated at the design points
vector of fitted values of the
TPSS fit evaluated at the design points 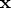 .
The
.
The 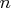 is the number of observations.
The final TPSS fit depends on the optional lambda.
is the number of observations.
The final TPSS fit depends on the optional lambda.
- coeff
- is a vector of spline coefficients.
The vector contains the coefficients for basis
functions in the null space and the representer
of evaluation functions at unique design points.
(Refer to Wahba 1990 for more detail on reproducing kernel
Hilbert space and representer of evaluation functions.)
The length of coeff vector depends on the number of unique
design points and the number of variables in the spline model.
In general, let nuobs and
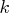 be the number of unique
rows and the number of columns of
be the number of unique
rows and the number of columns of 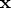 respectively.
The length of coeff equals to
respectively.
The length of coeff equals to 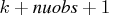 .
The coeff vector can be used as an input of TPSPLNEV
to evaluate the resulting TPSS fit at new data points.
.
The coeff vector can be used as an input of TPSPLNEV
to evaluate the resulting TPSS fit at new data points.
- adiag
- is an
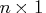 vector of diagonal
elements of the "hat" matrix.
See the "Details" section.
vector of diagonal
elements of the "hat" matrix.
See the "Details" section.
- gcv
- If lambda is not specified, then gcv is the minimum value of the GCV function. If lambda is specified, then gcv is a vector (or scalar if lambda is a scalar) of GCV values evaluated at the lambda points. It provides you with both the ability to study the GCV curves by plotting gcv against lambda and the chance to identify a possible local minimum.
The inputs to the TPSPLINE subroutine are as follows:
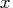
- is an
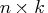 matrix of design
points on which the TPSS is to be fit.
The
matrix of design
points on which the TPSS is to be fit.
The 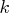 is the number of variables in the spline model.
The columns of
is the number of variables in the spline model.
The columns of 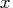 need to be linearly independent
and contain no constant column.
need to be linearly independent
and contain no constant column.
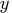
- is the
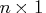 vector of observations.
vector of observations.
- lambda
- is a optional
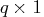 vector containing
vector containing
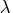 values in
values in 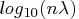 scale.
This option gives you the power to control how
you want the TPSPLINE subroutine to function.
If lambda is not specified (or lambda is
specified and
scale.
This option gives you the power to control how
you want the TPSPLINE subroutine to function.
If lambda is not specified (or lambda is
specified and 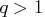 ) the GCV function is used to choose the
"best"
) the GCV function is used to choose the
"best" 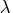 and the returning fitted values
are based on the
and the returning fitted values
are based on the 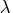 that minimizes the GCV function.
If lambda is specified and
that minimizes the GCV function.
If lambda is specified and 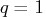 , no minimization
of the GCV function is involved and the fitted,
coeff and adiag values are all based
on the TPSS fit using this particular lambda.
This gives you the freedom to choose the
, no minimization
of the GCV function is involved and the fitted,
coeff and adiag values are all based
on the TPSS fit using this particular lambda.
This gives you the freedom to choose the
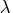 that you deem appropriate.
that you deem appropriate.
Aside from the values returned, the TPSPLINE subroutine also prints other useful information such as the number of unique observations, the dimensions of the null space, the number of parameters in the model, a GCV estimate of
Note: No missing values are accepted within the input arguments. Also, you should use caution if you want to specify small lambda values. Since the true
For convenience, the TPSS method is illustrated with a two-dimensional independent variable
Assume that the data are from the model
You measure the smoothness of
Let matrix
To evaluate the TPSS fit
Suppose
An example is given in the documentation for the TPSPLNEV call.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![j_2(f) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} [ \frac{\partial^2 f}... ...rtial {x_2}} ]^2 + [ \frac{\partial^2 f}{\partial {x_2}^2} ]^2 dx_1 dx_2](images/langref_langrefeq1269.gif)