Language Reference: TOEPLITZ Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

TOEPLITZ Function

generates a Toeplitz or block-Toeplitz matrix

TOEPLITZ( )

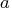where

is either a vector or a numeric matrix.

The TOEPLITZ function generates a Toeplitz matrix from a vector, or a block Toeplitz matrix from a matrix. A block Toeplitz matrix has the property that all matrices on the diagonals are the same. The argument

is an

matrix; the value returned is the

result.

The TOEPLITZ function uses the first

submatrix,

, of the argument matrix as the blocks of the main diagonal. The second

submatrix,

, of the argument matrix forms one secondary diagonal, with the transpose

forming the other. The remaining diagonals are formed accordingly. If the first

submatrix of the argument matrix is symmetric, the result is also symmetric. If

, the first

columns of the returned matrix,

, are the same as

. If

, the first

rows of

are the same as

. The TOEPLITZ function is especially useful in time series applications, where the covariance matrix of a set of variables with its lagged set of variables is often assumed to be a block Toeplitz matrix.

If

$a = [ a_1|{a}_2|{a}_3| ... |{a}_n ]$

and if

is the matrix formed by the TOEPLITZ function, then

$r = [ a_1 & | & a_2 & | & a_3 & | & ... & | & a_n \ a_2^' & | & a_1 & | ... ...& & & & & \ a_n^' & | & a_{n-1}^' & | & a_{n-2}^' & | & ... & | & a_1 ]$

$a = [ a_1 \ a_2 \ \vdots \ a_n \ ]$

and if

is the matrix formed by the TOEPLITZ function, then

$r = [ a_1 & | & a_2^' & | & a_3^' & | & ... & | & a_n^' \ a_2 & | & a_1 ... ...ts & & & & & & \ a_n & | & a_{n-1} & | & a_{n-2} & | & ... & | & a_1 ]$

Three examples follow.

  
     r=toeplitz(1:5);

  
              R             5 rows      5 cols    (numeric) 
  
                    1         2         3         4         5 
                    2         1         2         3         4 
                    3         2         1         2         3 
                    4         3         2         1         2 
                    5         4         3         2         1 
  
  
       r=toeplitz({1 2 , 
                   3 4 , 
                   5 6 , 
                   7 8}); 
  
                 R             4 rows      4 cols    (numeric) 
  
                            1         2         5         7 
                            3         4         6         8 
                            5         6         1         2 
                            7         8         3         4 
  
  
       r=toeplitz({1 2 3 4 , 
                   5 6 7 8}); 
  
                 R             4 rows      4 cols    (numeric) 
  
                            1         2         3         4 
                            5         6         7         8 
                            3         7         1         2 
                            4         8         5         6

Top of Page