Language Reference

SOLVELIN Call

solves a sparse symmetric linear system by direct decomposition

CALL SOLVELIN( x, status, A, b, method);

The SOLVELIN call returns the following values:

x

is the solution to .

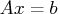status

is the final status of the solution.

The inputs to the SOLVELIN call are as follows:

A

is the sparse coefficient matrix in the equation .

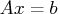b

is the right side of the equation .

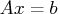method

is the name of the decomposition to be used.

The SOLVELIN call uses direct decomposition to solve sparse symmetric linear systems. The input matrix represents the coefficient matrix in sparse format; it is an by 3 matrix, where is the number of nonzero elements. The first column contains the nonzero values, while the second and third columns contain the row and column locations for the nonzero elements, respectively. Since is assumed to be symmetric, only the elements on and below the diagonal should be specified, and it is an error to specify elements above the diagonal.

The solution to the system is returned in . Your program should also check the returned to make sure that a solution was found.

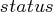= 0

indicates success.

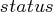= 1

indicates the matrix A is not positive-definite.

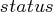= 2

indicates the system ran out of memory.

If the SOLVELIN call is unable to solve your system, you can try the iterative method call ITSOLVER.

Two different factorization methods are available from the call, Cholesky and Symbolic LDL, specified as 'CHOL' or 'LDL' with the parameter. Both these factorizations are applicable only to positive-definite symmetric systems; if your system is not positive-definite or not symmetric, you can use an ITSOLVER call.

The following example uses SOLVELIN to solve the system:

  
  
 /* value     row column */ 
 A = {  3       1      1, 
        1.1     2      1, 
        4       2      2, 
        1       3      2, 
        3.2     4      2, 
       10       3      3, 
        3       4      4}; 
  
 /* right hand side */ 
 b = {1, 1, 1, 1}; 
  
 call solvelin(x, status, A, b, 'LDL'); 
  
 print status x;
 

The results are as follows:

  
                  STATUS         X 
  
                       0      2.68 
                              -6.4 
                              0.74 
                              7.16