Language Reference

SOLVE Function

solves a system of linear equations

SOLVE( , )

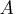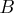The inputs to the SOLVE function are as follows:

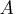
is an 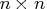nonsingular matrix.

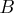
is an 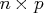matrix.

The SOLVE function solves the set of linear equations for . must be square and nonsingular.

is equivalent to using the INV function as . However, the SOLVE function is recommended over the INV function because it is more efficient and more accurate. An example follows:

  
    x=solve(a,b);
 

The solution method used is discussed in Forsythe, Malcolm, and Moler (1967).

The SOLVE function (as well as the DET and INV functions) uses the following criterion to decide whether the input matrix, , is singular:

where MACHEPS is the relative machine precision.

All matrix elements less than or equal to sing are now considered rounding errors of the largest matrix elements, so they are taken to be zero. For example, if a diagonal or triangular coefficient matrix has a diagonal value less than or equal to sing, the matrix is considered singular by the DET, INV, and SOLVE functions.

Previously, a much smaller singularity criterion was used, which caused algebraic operations to be performed on values that were essentially floating-point error. This occasionally yielded numerically unstable results. The new criterion is much more conservative, and it generates far fewer erroneous results. In some cases, you might need to scale the data to avoid singular matrices. If you think the new criterion is too strong, do the following:

• Try the GINV function to compute the generalized inverse.
• Examine the size of the singular values returned by the SVD function. The SVD function can be used to compute a generalized inverse with a user-specified singularity criterion.

If is an matrix, the SOLVE function temporarily allocates an array in addition to the memory allocated for the return matrix.