Language Reference: SVD Call :: SAS/IML(R) 9.2 User's Guide

Language Reference

SVD Call

computes the singular value decomposition

CALL SVD( , , , );

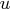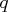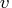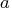In the SVD subroutine:

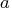
: is the input matrix that is decomposed as described in the following discussion.
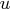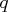, , and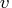: are the returned decomposition matrices.

The SVD subroutine decomposes a real

matrix

(where

is greater than or equal to

) into the form

$a= u* {diag}(q)*v^'$

where

$u^' u = v^' v = {vv}^' = i_n$

and

contains the singular values of

, and

.

When

is greater than or equal to

consists of the orthonormal eigenvectors of ${aa}^'$ , and

consists of the orthonormal eigenvectors of

contains the square roots of the eigenvalues of

and ${aa}^'$ , except for some zeros.

If

is less than

, a corresponding decomposition is done where

and

switch roles:

$a= u* {diag}(q)*v^'$

but

$u^' u = {uu}^' = v^' v = i_w$

The singular values are sorted in descending order.

For information about the method used in the SVD subroutine, refer to Wilkinson and Reinsch (1971). Consider the following example (Wilkinson and Reinsch 1971, p. 149):

  
    a={22  10   2   3   7, 
       14   7  10   0   8, 
       -1  13  -1 -11   3, 
       -3  -2  13  -2   4, 
        9   8   1  -2   4, 
        9   1  -7   5  -1, 
        2  -6   6   5   1, 
        4   5   0  -2   2}; 
    call svd(u,q,v,a); 
    reset fuzz; /* print small numbers as zero */ 
    zero = ssq(a - u*diag(q)*v`);

The matrix is rank-3 with exact singular values $\sqrt{1248}$ , 20, $\sqrt{384}$ , , and . Because of the repeated singular values, the last two columns of the U matrix are not uniquely determined. A valid result is the following:

  
       U             8 rows      5 cols    (numeric) 
  
     0.7071068 0.1581139 -0.176777 -0.212785 -0.560643 
     0.5303301 0.1581139 0.3535534 0.0801354 0.3127085 
     0.1767767 -0.790569 0.1767767  0.486821 -0.155628 
             0 0.1581139 0.7071068 0.1118328 -0.175184 
     0.3535534 -0.158114         0 -0.082888  0.348706 
     0.1767767 0.1581139  -0.53033 0.5984857 0.1586763 
             0 0.4743416 0.1767767 0.4882498 0.1463314 
     0.1767767 -0.158114         0 -0.308798 0.6039844 
  
  
        Q             5 rows      1 col     (numeric) 
  
                           35.327043 
                                  20 
                           19.595918 
                           1.113E-15 
                           5.079E-16 
  
         V             5 rows      5 cols    (numeric) 
  
       0.8006408 0.3162278 -0.288675 -0.419095         0 
       0.4803845 -0.632456         0 0.4405091 0.4185481 
       0.1601282 0.3162278 0.8660254 -0.052005 0.3487901 
               0 0.6324555 -0.288675 0.6760591  0.244153 
       0.3202563         0 0.2886751 0.4129773 -0.802217

The SVD routine performs most of its computations in the memory allocated for returning the singular value decomposition.

Top of Page