Language Reference

SWEEP Function

sweeps a matrix

SWEEP( matrix, index-vector)

The inputs to the SWEEP function are as follows:

matrix

is a numeric matrix or literal.

index-vector

is a numeric vector indicating the pivots.

The SWEEP function sweeps matrix on the pivots indicated in index-vector to produce a new matrix. The values of the index vector must be less than or equal to the number of rows or the number of columns in matrix, whichever is smaller.

For example, suppose that is partitioned into

such that is and is . Let

  
    I = [1 2 3 . . . q]
 

Then, the statement

  
    B=sweep(A,I);
 

becomes

The index vector can be omitted. In this case, the function sweeps the matrix on all pivots on the main diagonal 1:MIN(nrow,ncol).

The SWEEP function has sequential and reversibility properties when the submatrix swept is positive definite:

• SWEEP(SWEEP(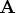,1),2)=SWEEP(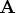,{ 1 2 })
• SWEEP(SWEEP(,),)=

See Beaton (1964) for more information about these properties.

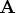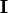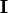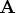
To use the SWEEP function for regression, suppose the matrix contains

where is .

Then contains

The partitions of form the beta values, SSE, and a matrix proportional to the covariance of the beta values for the least squares estimates of in the linear model

If any pivot becomes very close to zero (less than or equal to 1E-12), the row and column for that pivot are zeroed. See Goodnight (1979) for more information.

An example that uses the SWEEP function for regression follows:

  
    x = { 1  1  1, 
          1  2  4, 
          1  3  9, 
          1  4 16, 
          1  5 25, 
          1  6 36, 
          1  7 49, 
          1  8 64 }; 
  
    y = {  3.929, 
           5.308, 
           7.239, 
           9.638, 
          12.866, 
          17.069, 
          23.191, 
          31.443 }; 
  
    n = nrow(x);         /* number of observations */ 
    k = ncol(x);         /* number of variables */ 
    xy = x||y;           /* augment design matrix */ 
    A = xy` * xy;        /* form cross products */ 
    S = sweep( A, 1:k ); 
  
    beta = S[1:k,4];     /* parameter estimates */ 
    sse = S[4,4];        /* sum of squared errors */ 
    mse = sse / (n-k);   /* mean squared error */ 
    cov = S[1:k, 1:k] # mse; /* covariance of estimates */ 
    print cov, beta, sse; 
  
                              COV 
  
                 0.9323716 -0.436247 0.0427693 
                 -0.436247 0.2423596 -0.025662 
                 0.0427693 -0.025662 0.0028513 
  
  
                              BETA 
  
                           5.0693393 
                           -1.109935 
                           0.5396369 
  
  
                              SSE 
  
                           2.395083
 

The SWEEP function performs most of its computations in the memory allocated for the result matrix.