Language Reference: ITSOLVER Call :: SAS/IML(R) 9.2 User's Guide

Language Reference

ITSOLVER Call

solves a sparse linear system by using iterative methods

CALL ITSOLVER( x, error, iter, method, A, b, <precon>, <tol>, <maxiter>, <start>, <history>);

The ITSOLVER call returns the following values:

x: is the solution to .
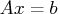error: is the final relative error of the solution.
iter: is the number of iterations executed.

The inputs to the ITSOLVER call are as follows:

method: is the type of iterative method to use.
A: is the sparse coefficient matrix in the equation .
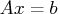b: is a column vector, the right side of the equation .
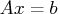precon: is the name of a preconditioning technique to use.
tol: is the relative error tolerance.
maxiter: is the iteration limit.
start: is a starting point column vector.
history: is a matrix to store the relative error at each iteration.

The ITSOLVER call solves a sparse linear system by iterative methods, which involve updating a trial solution over successive iterations to minimize the error. The ITSOLVER call uses the technique specified in the

parameter to update the solution. The accepted

options are as follows:

method = 'CG':: conjugate gradient algorithm, when A is symmetric and positive definite.
method = 'CGS':: conjugate gradient squared algorithm, for general A.
method = 'MINRES':: minimum residual algorithm, when A is symmetric indefinite.
method = 'BICG':: biconjugate gradient algorithm, for general A.

The input matrix

represents the coefficient matrix in sparse format; it is an

3 matrix, where

is the number of nonzero elements. The first column contains the nonzero values, while the second and third columns contain the row and column locations for the nonzero elements, respectively. For the algorithms assuming symmetric

, conjugate gradient, and minimum residual, only the lower triangular elements should be specified. The algorithm continues iterating to improve the solution until either the relative error tolerance specified in

is satisfied or the maximum number of iterations specified in

is reached. The relative error is defined as

$error = \vert ax - b\vert _2 / (\vert b \vert _2 + \epsilon )$

where the $\vert \cdot \vert _2$ operator is the Euclidean norm, and $\epsilon$ is a machine-dependent epsilon value to prevent any division by zero. If

is not specified in the call, then a default value of $10^{-7}$ is used for

and 100000 for

.

The convergence of an iterative algorithm can often be enhanced by preconditioning the input coefficient matrix. The preconditioning option is specified with the

parameter, which can take one of the following values:

precon = 'NONE':: no preconditioning
precon = 'IC':: incomplete Cholesky factorization, for 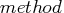= 'CG' or 'MINRES' only
precon = 'DIAG':: diagonal Jacobi preconditioner, for 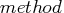= 'CG' or 'MINRES' only
precon = 'MILU':: modified incomplete LU factorization, for 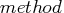= 'BICG' only

is not specified, no preconditioning is applied.

A starting trial solution can be specified with the

parameter; otherwise the ITSOLVER call generates a zero starting point. You can supply a matrix to store the relative error at each iteration with the

parameter. The

matrix should be dimensioned with enough elements to store the maximum number of iterations you expect.

Your IML program should always check the returned

and

parameters to verify that the desired relative error tolerance was reached. If not, your program might continue the solution process with another ITSOLVER call, with

set to the latest result. You might also try a different

option to enhance convergence.

For example, use the biconjugate gradient algorithm to solve the system

$[ 3 & 2 & 0 & 0 \ 1.1 & 4 & 1 & 3.2 \ 0 & 1 & -10 & 0 \ 0 & 3.2 & 0 & 3 ] x = [ 1 \ 1 \ 1 \ 1 ]$

Here is the code:

  
 /* value     row column */ 
 A = {  3       1      1, 
        2       1      2, 
        1.1     2      1, 
        4       2      2, 
        1       3      2, 
        3.2     4      2, 
       -10      3      3, 
        3       4      4}; 
  
 /* right hand side */ 
 b = {1, 1, 1, 1}; 
 maxiter = 10; 
 hist = j(maxiter,1,.); 
 start = {1,1,1,1}; 
 tol = 1e-10; 
 call itsolver(x, error, iter, 'bicg', A, b, 'milu', tol, 
               maxiter, start, hist); 
 print x; 
 print iter error; 
 print hist;

The results are as follows:

  
                        X 
  
                    0.2040816 
                    0.1938776 
                   -0.080612 
                    0.1265306 
  
  
               ITER     ERROR 
  
                  3 3.494E-16

Use the conjugate gradient algorithm solve the symmetric positive definite system

$[ 3 & 1.1 & 0 & 0 \ 1.1 & 4 & 1 & 3.2 \ 0 & 1 & 10 & 0 \ 0 & 3.2 & 0 & 3 ] x = [ 1 \ 1 \ 1 \ 1 ]$

Here is the code:

  
  
 /* value     row column */ 
 A = {  3       1      1, 
        1.1     2      1, 
        4       2      2, 
        1       3      2, 
        3.2     4      2, 
       10       3      3, 
        3       4      4}; 
  
 /* right hand side */ 
 b = {1, 1, 1, 1}; 
  
 call itsolver(x, error, iter, 'CG', A, b); 
  
 print x, iter, error;

The results are as follows:

Top of Page