| Language Reference |
IPF Call
performs an iterative proportional fit of a contingency table
- CALL IPF( fit, status, dim, table, config<, initab<, mod>);
The inputs to the IPF subroutine are as follows:
- fit
- is a returned matrix.
The matrix fit contains an array of
the estimates of the expected number in each
cell under the model specified in config.
This matrix conforms to table, meaning that it has the same
dimensions and order of variables.
- status
- is a returned matrix.
The status argument is a row vector of length 3.
status[1] is 0 if there is convergence to the
desired accuracy, otherwise it is nonzero.
status[2] is the maximum
difference between estimates of the last two iterations of the IPF
algorithm. status[3] is the number of iterations performed.
- dim
- is an input matrix.
If the problem contains
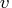variables then
dim is 
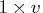row vector.
The value dim[i] is the number of
possible levels for variable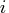 
in a contingency table.
- table
- is an input matrix.
The table argument specifies an array of the
number of observations at each level of each variable.
Variables are nested across columns and then across rows.
- config
- is an input matrix.
The config argument
specifies which marginal totals to fit.
Each column of config specifies a distinct marginal
in the model under consideration.
Because the model is hierarchical, all subsets
of specified marginals are included in fitting.
- initab
- is an input matrix.
The initab argument is an array of
initial values for the iterative procedure.
If you do not specify values, 1s are used.
For incomplete tables, initab is set to 1 if the
cell is included in the design, and 0 if it is not.
- mod
- is an input matrix. The mod argument is a two-element vector specifying the stopping criteria. If mod= {maxdev, maxit}, then the procedure iterates either until the maximum difference between estimates of the last two iterations is less than maxdev or until maxit iterations are completed. Default values are maxdev=0.25 and maxit=15.
The IPF subroutine performs an iterative proportional fit of a contingency table. This is a standard statistical technique to obtain maximum likelihood estimates for cells under any hierarchical log-linear model. The algorithm is described in Bishop, Fienberg, and Holland (1975).
The matrix table must conform in size to the contingency table as specified in dim. In particular, if table is
, the
product of the entries in dim must equal 
.
Furthermore, there must be some integer 
such that the
product of the first entries in dim equals 
.
If you specify initab, then it
must be the same size as table.
Adjusting a Table from Marginals
A common use of the IPF algorithm is to adjust the entries of a table in order to fit a new set of marginals while retaining the interaction between cell entries.
Example 1: Adjusting Marital Status by Age
Bishop, Fienberg, and Holland (1975) present data from D. Friedlander showing the distribution of women in England and Wales according to their marital status in 1957. One year later, new official marginal estimates were announced. The problem is to adjust the entries in the 1957 table so as to fit the new marginals while retaining the interaction between cells. This problem can arise when you have internal cells that are known from sampling a population, and then get margins based on a complete census.
When you want to adjust an observed table of cell frequencies to a new set of margins, you must set the initab parameter to be the table of observed values. The new marginals are specified through the table argument. The particular cell values for table are not important, since only the marginals will be used (the proportionality between cells is determined by initab).
There are two easy ways to create a table that contains given margins. Recall that a table of independent variables has an expected cell value
. Thus you could form a table with
these cell entries. Another possibility is to use a ``greedy
algorithm'' to assign as many of the marginals as possible to the
first cell, then assign as many of the remaining marginals as possible to the
second cell, and so on until all of the marginals have been
distributed. Both of these approaches are encapsulated into modules in
the following program:
/* Return a table such that cell (i,j) has value
(sum of row i)(sum of col j)/(sum of all cells) */
start GetIndepTableFromMargins( bottom, side );
if bottom[+] ^= side[+] then do;
print "Marginal totals are not equal";
abort;
end;
table = side*bottom/side[+];
return (table);
finish;
/* Use a "greedy" algorithm to create a table whose
marginal totals match given marginal totals.
Margin1 is the vector of frequencies totaled down
each column. Margin1 means that
Variable 1 has NOT been summed over.
Margin2 is the vector of frequencies totaled across
each row. Margin2 means that Variable 2
has NOT been summed over.
After calling, use SHAPE to change the shape of
the returned argument. */
start GetGreedyTableFromMargins( Margin1, Margin2 );
/* copy arguments so they are not corrupted */
m1 = colvec(Margin1); /* colvec is in IMLMLIB */
m2 = colvec(Margin2);
if m1[+] ^= m2[+] then do;
print "Marginal totals are not equal";
abort;
end;
dim1 = nrow(m1);
dim2 = nrow(m2);
table = j(1,dim1*dim2,0);
/* give as much to cell (1,1) as possible,
then as much as remains to cell (1,2), etc,
until all the margins have been distributed */
idx = 1;
do i2 = 1 to dim2;
do i1 = 1 to dim1;
t = min(m1[i1],m2[i2]);
table[idx] = t;
idx = idx + 1;
m1[i1] = m1[i1]-t;
m2[i2] = m2[i2]-t;
end;
end;
return (table);
finish;
Mod = {0.01 15}; /* tighten stopping criterion */
Columns = {' Single' ' Married' 'Widow/Divorced'};
Rows = {'15 - 19' '20 - 24' '25 - 29' '30 - 34'
'35 - 39' '40 - 44' '45 - 49' '50 Or Over'};
/* Marital status has 3 levels. Age has 8 levels */
Dim = {3 8};
/* Use known distribution for start-up values */
IniTab = { 1306 83 0 ,
619 765 3 ,
263 1194 9 ,
173 1372 28 ,
171 1393 51 ,
159 1372 81 ,
208 1350 108 ,
1116 4100 2329 };
/* New marginal totals for age by marital status */
NewMarital = { 3988 11702 2634 };
NewAge = {1412,1402,1450,1541,1681,1532,1662,7644};
/* Create any table with these marginals */
Table = GetGreedyTableFromMargins(NewMarital, NewAge);
Table = shape(Table, nrow(IniTab), ncol(IniTab));
/* Consider all main effects */
Config = {1 2};
call ipf(Fit,Status,Dim,Table,Config,IniTab,Mod);
if Status[1] = 0 then
print 'Known Distribution (1957)',
IniTab [colname=Columns rowname=Rows format=8.0],,
'Adjusted Estimates Of Distribution (1958)',
Fit [colname=Columns rowname=Rows format=8.2];
else
print "IPF did not converge in "
(Status[3]) " iterations";
The results of this program are as follows. The same results are obtained if the table parameter is formed by using the "independent algorithm."
Known Distribution (1957)
INITAB
Single Married Widow/Divorced
15 - 19 1306 83 0
20 - 24 619 765 3
25 - 29 263 1194 9
30 - 34 173 1372 28
35 - 39 171 1393 51
40 - 44 159 1372 81
45 - 49 208 1350 108
50 Or Over 1116 4100 2329
Adjusted Estimates Of Distribution (1958)
FIT
Single Married Widow/Divorced
15 - 19 1325.27 86.73 0.00
20 - 24 615.56 783.39 3.05
25 - 29 253.94 1187.18 8.88
30 - 34 165.13 1348.55 27.32
35 - 39 173.41 1454.71 52.87
40 - 44 147.21 1308.12 76.67
45 - 49 202.33 1352.28 107.40
50 Or Over 1105.16 4181.04 2357.81
Example 2: Adjusting Votes by Region
A similar technique can be used to standardize data from raw counts into percentages. For example, consider data from a 1836 vote in the U.S. House of Representatives on a resolution that the House should adopt a policy of tabling all petitions for the abolition of slavery. Attitudes toward abolition were different among slaveholding states that would later secede from the Union ("the South"), slaveholding states that refused to secede (``the Border States''), and nonslaveholding states ("the North").
The raw votes for the resolution are defined in the following code. The data are hard to interpret because the margins are not homogeneous.
/* Yea Abstain Nay */
IniTab = { 61 12 60, /* North */
17 6 1, /* Border */
39 22 7 }; /* South */
Standardizing the data by specifying homogeneous margins reveals interactions and symmetry that were not apparent in the raw data. Suppose the margins are specified as follows:
NewVotes = {100 100 100};
NewSection = {100,100,100};
In this case, the program for marital status by age can be easily rewritten to adjust the votes into a standardized form. The resulting output is as follows:
FIT
Yea Abstain Nay
North 20.1 10.2 69.7
Border 47.4 42.8 9.8
South 32.5 47.0 20.5
Generating a Table with Given Marginals
The "greedy algorithm" presented in the Marital-Status-By-Age example can be extended in a natural way to the case where you have
1-way marginals and want to form an -dimensional table. For
example, a three-dimensional "greedy algorithm" would allocate the
vector table as table=j(dim1*dim2*dim3,1,0); and have
three nested loops as indicated in the following code. Afterwards the
table parameter can be reshaped by using the SHAPE
function.
do i3 = 1 to dim3;
do i2 = 1 to dim2;
do i1 = 1 to dim1;
t = min(m1[i1],m2[i2],m3[i3]);
table[idx] = t;
idx = idx + 1;
m1[i1] = m1[i1]-t;
m2[i2] = m2[i2]-t;
m3[i3] = m3[i3]-t;
end;
end;
end;
The idea of the "greedy algorithm" can be extended to marginals that are not 1-way. For example, the following three-dimensional table is similar to one appearing in Christensen (1997) based on data from M. Rosenberg. The table presents data on a person's self-esteem for people classified according to their religion and their father's educational level.
| Father's Educational Level | ||||||
| Self- | Not HS | HS | Some | Coll | Post | |
| Religion | Esteem | Grad | Grad | Coll | Grad | Coll |
| High | 575 | 388 | 100 | 77 | 51 | |
| Catholic | ||||||
| Low | 267 | 153 | 40 | 37 | 19 | |
| High | 117 | 102 | 67 | 87 | 62 | |
| Jewish | ||||||
| Low | 48 | 35 | 18 | 12 | 13 | |
| High | 359 | 233 | 109 | 197 | 90 | |
| Protestant | ||||||
| Low | 159 | 173 | 47 | 82 | 32 | |
Since the father's education level is nested across columns, it is Variable 1 with levels corresponding to not finishing high school, graduating from high school, attending college, graduating from college, and attending graduate courses. The variable that varies the quickest across rows is Self-Esteem, so Self-Esteem is Variable 2 with values "High" and "Low." The Religion variable is Variable 3 with values "Catholic," "Jewish," and "Protestant."
The following program encodes this table, using the MARG call to compute a 2-way marginal table by summing over the third variable and a 1-way marginal by summing over the first two variables. Then a new table (NewTable) is created by applying the greedy algorithm to the two marginals. Finally, the marginals of NewTable are computed and compared with those of table.
dim={5 2 3};
table={
/* Father's Education:
NotHSGrad HSGrad Col ColGrad PostCol
Self-
Relig Esteem */
/* Cath- Hi */ 575 388 100 77 51,
/* olic Lo */ 267 153 40 37 19,
/* Jew- Hi */ 117 102 67 87 62,
/* ish Lo */ 48 35 18 12 13,
/* Prote- Hi */ 359 233 109 197 90,
/* stant Lo */ 159 173 47 82 32
};
config = { 1 3,
2 0 };
call marg(locmar, marginal, dim, table, config);
print locmar, marginal, table;
/* Examine marginals: The name indicates the
variable(s) that are NOT summed over.
The locmar variable tells where to index
into the marginal variable. */
Var12_Marg = marginal[1:(locmar[2]-1)];
Var12_Marg = shape(Var12_Marg,dim[2],dim[1]);
Var3_Marg = marginal[locMar[2]:ncol(marginal)];
NewTable = j(nrow(table),ncol(table),0);
/* give as much to cell (1,1,1) as possible,
then as much as remains to cell (1,1,2), etc,
until all the margins have been distributed. */
idx = 1;
do i3 = 1 to dim[3]; /* over Var3 */
do i2 = 1 to dim[2]; /* over Var2 */
do i1 = 1 to dim[1]; /* over Var1 */
/* Note Var12_Marg has Var1 varying across
the columns */
t = min(Var12_Marg[i2,i1],Var3_Marg[i3]);
NewTable[idx] = t;
idx = idx + 1;
Var12_Marg[i2,i1] = Var12_Marg[i2,i1]-t;
Var3_Marg[i3] = Var3_Marg[i3]-t;
end;
end;
end;
call marg(locmar, NewMarginal, dim, table, config);
maxDiff = abs(marginal-NewMarginal)[<>];
if maxDiff=0 then
print "Marginals are unchanged";
print NewTable;
The results of this program are as follows:
LOCMAR
1 11
MARGINAL
COL1 COL2 COL3 COL4 COL5 COL6 COL7
ROW1 1051 723 276 361 203 474 361
MARGINAL
COL8 COL9 COL10 COL11 COL12 COL13
ROW1 105 131 64 1707 561 1481
TABLE
575 388 100 77 51
267 153 40 37 19
117 102 67 87 62
48 35 18 12 13
359 233 109 197 90
159 173 47 82 32
Marginals are unchanged
NEWTABLE
1051 656 0 0 0
0 0 0 0 0
0 67 276 218 0
0 0 0 0 0
0 0 0 143 203
474 361 105 131 64
Fitting a Log-Linear Model to a Table
A second common usage of the IPF algorithm is to hypothesize that the table of observations can be fitted by a model with known effects and to ask whether the observed values indicate that the model hypothesis can be accepted or should be rejected. In this usage, you normally do not specify the initab argument to IPF (but see the comment on structural zeros in the section "Additional Details").
Korff, Taback, and Beard (1952) reported statistics related to the outbreak of food poisoning at a company picnic. A total of 304 people at the picnic were surveyed to determine who had eaten either of two suspect foods: potato salad and crabmeat. The predictor variables are whether the individual ate potato salad (Variable 1: "Yes" or "No") and whether the person ate crabmeat (Variable 2: "Yes" or "No"). The response variable is whether the person was ill (Variable 3: "Ill" or "Not Ill"). The order of the variables is determined by the dim and table arguments to IPF. The variables are nested across columns, then across rows.
| Crabmeat: | Y E S | N O | |||
| Potato salad: | Yes | No | Yes | No | |
| Ill | 120 | 4 | 22 | 0 | |
| Not Ill | 80 | 31 | 24 | 23 | |
The following program defines the variables and observations, and then fits three separate models. How well each model fits the data is determined by computing a Pearson chi-square statistic
, where
the sum is over all cells, 
stands for the observed cell count,
and 
stands for the fitted estimate. Other statistics,
such as the likelihood-ratio chi-square statistic 
, could also be used.
The program first fits a model that excludes the three-way interaction. The model fits well, so you can conclude that an association between illness and potato salad does not depend on whether an individual ate crabmeat. The next model excludes the interaction between potato salad and illness. This model is rejected with a large chi-square value, so the data support an association between potato salad and illness. The last model excludes the interaction between the crabmeat and the illness. This model fits moderately well. Here is the code:
/* Compute a chi-square score for a table of observed
values, given a table of expected values. Compare
this score to a chi-square value with given degrees
of freedom at 95% confidence level. */
start ChiSqTest( obs, model, degFreedom );
diff = (obs - model)##2 / model;
chiSq = diff[+];
chiSqCutoff = cinv(0.95, degFreedom);
print chiSq chiSqCutoff;
if chiSq > chiSqCutoff then
print "Reject hypothesis";
else
print "No evidence to reject hypothesis";
finish;
dim={2 2 2};
/* Crab meat: Y E S N O
Potato: Yes No Yes No */
table={ 120 4 22 0, /* Ill */
80 31 24 23 }; /* Not Ill */
crabmeat = " C R A B N O C R A B";
potato = {'YesPot' 'NoPot' 'YesPot' 'NoPot'};
illness = {'Ill', 'Not Ill'};
hypoth = "Hypothesis: no three-factor interaction";
config={1 1 2,
2 3 3};
call ipf(fit,status,dim,table,config);
print hypoth, "Fitted Model:",
fit[label=crabmeat colname=potato
rowname=illness format=6.2];
run ChiSqTest(table, fit, 1); /* 1 deg of freedom */
/* Test for interaction between Var 3 (Illness) and
Var 1 (Potato Salad) */
hypoth = "Hypothesis: no Illness-Potato Interaction";
config={1 2,
2 3};
call ipf(fit,status,dim,table,config);
print hypoth, "Fitted Model:",
fit[label=crabmeat colname=potato
rowname=illness format=6.2];
run ChiSqTest(table, fit, 2); /* 2 deg of freedom */
/* Test for interaction between Var 3 (Illness) and
Var 2 (Crab meat) */
hypoth = "Hypothesis: no Illness-Crab Interaction";
config={1 1,
2 3};
call ipf(fit,status,dim,table,config);
print hypoth, "Fitted Model:",
fit[label=crabmeat colname=potato
rowname=illness format=6.2];
run ChiSqTest(table, fit, 2); /* 2 deg of freedom */
The associated output is as follows:
HYPOTH
Hypothesis: no three-factor interaction
Fitted Model:
C R A B N O C R A B
YesPot NoPot YesPot NoPot
Ill 121.08 2.92 20.92 1.08
Not Ill 78.92 32.08 25.07 21.93
CHISQ CHISQCUTOFF
1.7021335 3.8414588
No evidence to reject hypothesis
HYPOTH
Hypothesis: no interaction between Illness and Potatoes
Fitted Model:
C R A B N O C R A B
YesPot NoPot YesPot NoPot
Ill 105.53 18.47 14.67 7.33
Not Ill 94.47 16.53 31.33 15.67
CHISQ CHISQCUTOFF
44.344643 5.9914645
Reject hypothesis
HYPOTH
Hypothesis: no interaction between Illness and Crab
Fitted Model:
C R A B N O C R A B
YesPot NoPot YesPot NoPot
Ill 115.45 2.41 26.55 1.59
Not Ill 84.55 32.59 19.45 21.41
CHISQ CHISQCUTOFF
5.0945132 5.9914645
No evidence to reject hypothesis
Additional Details
A few additional comments on the examples are in order.- Structural versus Random Zeros
- In the marriage-by-age example, the initab argument contained a zero for the "15-19 and Widowed/Divorced" category. Because the initab parameter determines the proportionality between cells, the fitted model retains a zero in that category. By contrast, in the potato-crab-illness example, the table parameter contained a zero for number of illnesses observed among those who did not eat either crabmeat or potato salad. This is a sampling (or random) zero. Some models preserve that zero; others do not. If your table has a structural zero (for example, the number of ovarian cancers observed among male patients), then you can use the initab parameter to preserve that zero. Refer to Bishop, Fienberg, and Holland (1975) or the documentation for the CATMOD procedure in SAS/STAT for more information about structural zeros and incomplete tables.
- The config Parameter
- The columns of this matrix specify which interaction effects should be
included in the model. The following table gives the model and the
configuration parameter for common interactions for an
table in three dimensions. The so-called
noncomprehensive models that do not include all variables (for
example, config = {1}) are not listed in the table, but
can be used. You can also specify combinations of main and interaction
effects. For example, config = {1 3, 2 0}) specifies all
main effects and the 1-2 interaction. Bishop, Fienberg, and Holland
(1975) and Christensen (1997) explain how to compute the degrees of
freedom associated with any model. For models with structural zeros,
computing the degrees of freedom is complicated.
Model Config Degrees of Freedom No three-factor {1 1 2,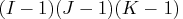 
2 3 3} One two-factor absent {1 2, 3 3}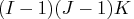 
{1 2, 2 3}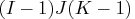 
{1 1, 2 3}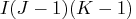 
Two two-factor absent {2, 3}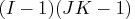 
{1, 3}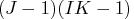 
{1, 2}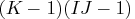 
No two-factor {1 2 3}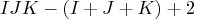 
Saturated {1,2,3}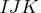 
- The Shape of the table Parameter
- Since variables are nested across columns and then across rows, any
shape that conforms to the dim parameter is equivalent.
For example, the section "Generating a Table with Given Marginals" presents data on a person's self-esteem for people classified according to their religion and their father's educational level. To save space, the educational levels are subsequently denoted by labels indicating the typical number of years spent in school: "<12," "12," "<16," "16," and ">16."
The table would be encoded as follows:dim={5 2 3}; table={ /* Father's Education: <12 12 <16 16 >16 Self- Relig Esteem */ /* Cath- Hi */ 575 388 100 77 51, /* olic Lo */ 267 153 40 37 19, /* Jew- Hi */ 117 102 67 87 62, /* ish Lo */ 48 35 18 12 13, /* Prote- Hi */ 359 233 109 197 90, /* stant Lo */ 159 173 47 82 32 };
The same information for the same variables in the same order could also be encoded into an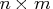 table in two other ways. Recall
that the product of entries in dim is 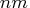and that 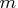must
equal the product of the first 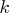entries of dim for some
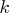. For this example, the product of the entries in dim is
30, and so the table must be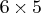 
, 
, or 
. The table is encoded as concatenating rows
1 - 2, 3 - 4, and 5 - 6 to produce the following:
table={ /* Esteem: H I G H L O W */ /* <12 ... >16 <12 ... >16 */ 575 ... 51 267 ... 19, /* Catholic */ 117 ... 62 48 ... 13, /* Jewish */ 359 ... 90 159 ... 32 /* Protestant*/ };
The table is encoded by concatenating all
rows, as follows:
table={ /* CATHOLIC ... PROTESTANT High Low ... High Low <12 ... >16 <12 ... >16 ... <12 ... >16 <12 ... >16 */ 575 ... 51 267 ... 19 ... 359 ... 90 159 ... 32 };
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.