The HPPANEL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specifying the Input DataSpecifying the Regression ModelSpecifying the Number of Nodes and Number of ThreadsUnbalanced DataOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsOne-Way Random-Effects ModelTwo-Way Random-Effects ModelBetween EstimatorsPooled EstimatorLinear Hypothesis TestingSpecification TestsOUTPUT OUT= Data SetOUTEST= Data SetPrinted OutputODS Table Names
Specifying the Input DataSpecifying the Regression ModelSpecifying the Number of Nodes and Number of ThreadsUnbalanced DataOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsOne-Way Random-Effects ModelTwo-Way Random-Effects ModelBetween EstimatorsPooled EstimatorLinear Hypothesis TestingSpecification TestsOUTPUT OUT= Data SetOUTEST= Data SetPrinted OutputODS Table Names -
Example

- References
One-Way Random-Effects Model
The specification for the one-way random-effects model is
![\[ u_{it}={\nu }_{i}+{\epsilon }_{it} \]](images/etsug_hppanel0080.png)
Let 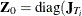 ),
),  , and
, and 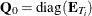 , with
, with 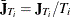 and
and 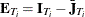 . Define
. Define 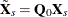 . Also define
. Also define 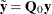 and
and  as a vector of 1s whose length is
as a vector of 1s whose length is  .
.
In the one-way model, estimation proceeds in a two-step fashion. First, you obtain estimates of the variance of the 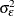 and
and 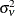 . There are multiple ways to derive these estimates; PROC HPPANEL provides four options. For more information, see the section
One-Way Random-Effects Model.
. There are multiple ways to derive these estimates; PROC HPPANEL provides four options. For more information, see the section
One-Way Random-Effects Model.
After the variance components are calculated from any method, the next task is to estimate the regression model of interest.
For each individual, you form a weight (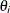 ),
),
![\[ \theta _\mi {i} = 1 - \sigma _{\epsilon } / w_\mi {i} \]](images/etsug_hppanel0092.png)
![\[ w_{i}^{2} = T_{i}{\sigma }^{2}_{{\nu }} + {\sigma }^{2}_{{\epsilon }} \]](images/etsug_hppanel0093.png)
where 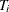 is the
is the 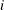 th cross section’s time observations.
th cross section’s time observations.
Taking the 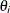 , you form the partial deviations,
, you form the partial deviations,
![\[ \tilde{y}_\mi {it} = y_\mi {it}- \theta _\mi {i} \bar{y}_\mi {i \cdot } \]](images/etsug_hppanel0096.png)
![\[ \tilde{x}_\mi {it} = x_\mi {it}- \theta _\mi {i} \bar{x}_\mi {i \cdot } \]](images/etsug_hppanel0097.png)
where 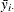 and
and 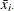 are cross section means of the dependent variable and independent variables (including the constant if any), respectively.
are cross section means of the dependent variable and independent variables (including the constant if any), respectively.
The random-effects 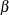 is then the result of simple OLS on the transformed data.
is then the result of simple OLS on the transformed data.