The COUNTREG Procedure
- Overview
- Getting Started
-
Syntax
 Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSPATIALDISPEFFECTS StatementSPATIALEFFECTS StatementSPATIALID StatementSPATIALZEROEFFECTS StatementSTORE StatementTEST StatementWEIGHT StatementZEROMODEL Statement
Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSPATIALDISPEFFECTS StatementSPATIALEFFECTS StatementSPATIALID StatementSPATIALZEROEFFECTS StatementSTORE StatementTEST StatementWEIGHT StatementZEROMODEL Statement -
Details
 Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionSpatial Lag of X ModelVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreParameter Naming Conventions for the RESTRICT, TEST, BOUNDS, and INIT StatementsComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmMarginal LikelihoodOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics
Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionSpatial Lag of X ModelVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreParameter Naming Conventions for the RESTRICT, TEST, BOUNDS, and INIT StatementsComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmMarginal LikelihoodOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics -
Examples

- References
Panel Data Analysis
Panel Data Poisson Regression with Fixed Effects
The count regression model for panel data can be derived from the Poisson regression model. Consider the multiplicative one-way panel data model,
![\[ y_{it} \sim \mbox{Poisson}(\mu _{it}) \]](images/etsug_countreg0292.png)
where
![\[ \mu _{it} = \alpha _{i} \lambda _{it} = \alpha _{i} \exp (\mathbf{x}_{it}’\bbeta ),\; \; i=1,\ldots ,N, \; \; t=1,\ldots ,T \]](images/etsug_countreg0293.png)
Here, 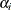 are the individual effects.
are the individual effects.
In the fixed-effects model, the 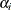 are unknown parameters. The fixed-effects model can be estimated by eliminating
are unknown parameters. The fixed-effects model can be estimated by eliminating 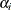 by conditioning on
by conditioning on 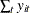 .
.
In the random-effects model, the 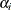 are independent and identically distributed (iid) random variables, in contrast to the fixed effects model. The random-effects
model can then be estimated by assuming a distribution for
are independent and identically distributed (iid) random variables, in contrast to the fixed effects model. The random-effects
model can then be estimated by assuming a distribution for 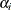 .
.
In the Poisson fixed-effects model, conditional on 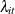 and parameter
and parameter 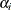 ,
, 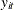 is iid Poisson-distributed with parameter
is iid Poisson-distributed with parameter 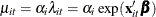 , and
, and 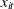 does not include an intercept. Then, the conditional joint density for the outcomes within the ith panel is
does not include an intercept. Then, the conditional joint density for the outcomes within the ith panel is
![\begin{eqnarray*} P[y_{i1},\ldots ,y_{iT_{i}}|\sum _{t=1}^{T_{i}}y_{it}] & = & P[y_{i1},\ldots ,y_{iT_{i}},\sum _{t=1}^{T_{i}}y_{it}] / P[\sum _{t=1}^{T_{i}}y_{it}] \\ & = & P[y_{i1},\ldots ,y_{iT_{i}}]/P[\sum _{t=1}^{T_{i}}y_{it}] \end{eqnarray*}](images/etsug_countreg0300.png)
Because 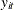 is iid Poisson(
is iid Poisson(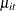 ),
), ![$P[y_{i1},\ldots ,y_{iT_{i}}]$](images/etsug_countreg0302.png) is the product of
is the product of 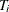 Poisson densities. Also,
Poisson densities. Also, 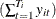 is Poisson(
is Poisson(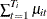 ). Then,
). Then,
![\begin{eqnarray*} P[y_{i1},\ldots ,y_{iT_{i}}|\sum _{t=1}^{T_{i}}y_{it}] & = & \frac{\sum _{t=1}^{T_{i}} (\exp (-\mu _{it}) \mu _{it}^{y_{it}} / y_{it}! )}{\exp (-\sum _{t=1}^{T_{i}} \mu _{it}) \left( \sum _{t=1}^{T_{i}} \mu _{it} \right)^{\sum _{t=1}^{T_{i}} y_{it} } / \left( \sum _{t=1}^{T_{i}} y_{it} \right)!} \\ & = & \frac{\exp (-\sum _{t=1}^{T_{i}} \mu _{it}) \left( \prod _{t=1}^{T_{i}} \mu _{it}^{y_{it}} \right) \left( \prod _{t=1}^{T_{i}} y_{it}! \right) }{\exp ( -\sum _{t=1}^{T_{i}} \mu _{it}) \prod _{t=1}^{T_{i}} \left( \sum _{s=1}^{T_{i}} \mu _{is} \right)^{y_{it}} / \left( \sum _{t=1}^{T_{i}} y_{it} \right)!} \\ & = & \frac{(\sum _{t=1}^{T_{i}} y_{it})!}{(\prod _{t=1}^{T_{i}} y_{it}!)} \prod _{t=1}^{T_{i}} \left(\frac{\mu _{it}}{\sum _{s=1}^{T_{i}} \mu _{is}}\right)^{y_{it}} \\ & = & \frac{(\sum _{t=1}^{T_{i}} y_{it})!}{(\prod _{t=1}^{T_{i}} y_{it}!)} \prod _{t=1}^{T_{i}} \left(\frac{\lambda _{it}}{\sum _{s=1}^{T_{i}} \lambda _{is}}\right)^{y_{it}} \\ \end{eqnarray*}](images/etsug_countreg0306.png)
Thus, the conditional log-likelihood function of the fixed-effects Poisson model is given by
![\[ \mathcal{L} = \sum _{i=1}^{N} \left[ \ln \left( (\sum _{t=1}^{T_{i}}y_{it})! \right) - \sum _{t=1}^{T_{i}}\ln (y_{it}!) + \sum _{t=1}^{T_{i}}y_{it}\ln \left(\frac{\lambda _{it}}{\sum _{s=1}^{T_{i}}\lambda _{is}}\right) \right] \]](images/etsug_countreg0307.png)
The gradient is
![\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial \bbeta } & = & \sum _{i=1}^{N} \sum _{t=1}^{T_{i}} y_{it}x_{it} - \sum _{i=1}^{N} \sum _{t=1}^{T_{i}} \left[ \frac{y_{it} \sum _{s=1}^{T_{i}} \left( \exp (\mathbf{x}_{is}'\bbeta ) \mathbf{x}_{is} \right)}{\sum _{s=1}^{T_{i}} \exp (\mathbf{x}_{is}'\bbeta )} \right] \\ & = & \sum _{i=1}^{N} \sum _{t=1}^{T_{i}} y_{it} (\mathbf{x}_{it}-\mathbf{\bar{x}}_{i}) \end{eqnarray*}](images/etsug_countreg0308.png)
where
![\[ \mathbf{\bar{x}}_{i} = \sum _{s=1}^{T_{i}} \left( \frac{\exp (\mathbf{x}_{is}'\bbeta )}{\sum _{k=1}^{T_{i}} \exp (\mathbf{x}_{ik}'\bbeta )} \right) \mathbf{x}_{is} \]](images/etsug_countreg0309.png)
Panel Data Poisson Regression with Random Effects
In the Poisson random-effects model, conditional on 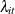 and parameter
and parameter 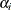 ,
, 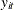 is iid Poisson-distributed with parameter
is iid Poisson-distributed with parameter 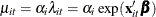 , and the individual effects,
, and the individual effects, 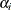 , are assumed to be iid random variables. The joint density for observations in all time periods for the ith individual,
, are assumed to be iid random variables. The joint density for observations in all time periods for the ith individual, ![$P[y_{i1},\ldots ,y_{iT}|\lambda _{i1},\ldots ,\lambda _{iT_{i}}]$](images/etsug_countreg0310.png) , can be obtained after the density
, can be obtained after the density 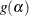 of
of 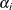 is specified.
is specified.
Let
![\[ \alpha _{i} \sim \mbox{iid}\; \mathrm{gamma}(\theta ,\theta ) \]](images/etsug_countreg0313.png)
so that 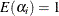 and
and 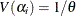 :
:
![\[ g(\alpha _{i}) = \frac{\theta ^{\theta }}{\Gamma (\theta )} \alpha _{i}^{\theta -1}\exp (-\theta \alpha _{i}) \]](images/etsug_countreg0316.png)
Let 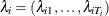 . Because
. Because 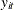 is conditional on
is conditional on 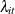 and parameter
and parameter 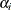 is iid Poisson(
is iid Poisson(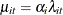 ), the conditional joint probability for observations in all time periods for the ith individual,
), the conditional joint probability for observations in all time periods for the ith individual, ![$P[y_{i1},\ldots ,y_{iT_{i}}|\lambda _{i},\alpha _{i}]$](images/etsug_countreg0319.png) , is the product of
, is the product of 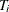 Poisson densities:
Poisson densities:
![\begin{eqnarray*} P[y_{i1},\ldots ,y_{iT_{i}}|\lambda _{i},\alpha _{i}] & = & \prod _{t=1}^{T_{i}} P[y_{it}| \lambda _{i}, \alpha _{i}]\\ & = & \prod _{t=1}^{T_{i}}\left[ \frac{\exp (-\mu _{it}) \mu _{it}^{y_{it}}}{y_{it}!} \right] \\ & = & \left[ \prod _{t=1}^{T_{i}} \frac{e^{-\alpha _{i}\lambda _{it}}(\alpha _{i}\lambda _{it})^{y_{it}}}{y_{it}!} \right] \\ & = & \left[ \prod _{t=1}^{T_{i}} \lambda _{it}^{y_{it}}/y_{it}! \right] \left( e^{-\alpha _{i} \sum _{t} \lambda _{it}} \alpha _{i}^{\sum _{t} y_{it}} \right) \end{eqnarray*}](images/etsug_countreg0320.png)
Then, the joint density for the ith panel conditional on just the 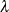 can be obtained by integrating out
can be obtained by integrating out 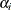 :
:
![\begin{eqnarray*} P[y_{i1},\ldots ,y_{iT_{i}}|\lambda _{i}] & = & \int _{0}^{\infty } P[y_{i1},\ldots ,y_{iT}|\lambda _{i},\alpha _{i}] g(\alpha _{i}) d\alpha _{i} \\ & = & \frac{\theta ^{\theta }}{\Gamma (\theta )} \left[ \prod _{t=1}^{T_{i}} \frac{\lambda _{it}^{y_{it}}}{y_{it}!} \right] \int _{0}^{\infty } \exp (-\alpha _{i} \sum _{t} \lambda _{it}) \alpha _{i}^{\sum _{t} y_{it}} \alpha _{i}^{\theta -1} \exp (-\theta \alpha _{i}) d\alpha _{i} \\ & = & \frac{\theta ^{\theta }}{\Gamma (\theta )} \left[ \prod _{t=1}^{T_{i}} \frac{\lambda _{it}^{y_{it}}}{y_{it}!} \right] \int _{0}^{\infty } \exp \left[ -\alpha _{i} \left( \theta + \sum _{t} \lambda _{it} \right) \right] \alpha _{i}^{\theta + \sum _{t} y_{it}-1} d\alpha _{i} \\ & = & \left[ \prod _{t=1}^{T_{i}} \frac{\lambda _{it}^{y_{it}}}{y_{it}!} \right] \frac{\Gamma (\theta + \sum _{t} y_{it})}{\Gamma (\theta )} \\ & & \times \left(\frac{\theta }{\theta +\sum _{t} \lambda _{it}} \right)^{\theta } \left(\theta + \sum _{t} \lambda _{it} \right)^{-\sum _{t} y_{it}} \\ & = & \left[ \prod _{t=1}^{T_{i}} \frac{\lambda _{it}^{y_{it}}}{y_{it}!} \right] \frac{\Gamma (\alpha ^{-1}+ \sum _{t} y_{it})}{\Gamma (\alpha ^{-1})} \\ & & \times \left(\frac{\alpha ^{-1}}{\alpha ^{-1}+\sum _{t} \lambda _{it}} \right)^{\alpha ^{-1}} \left(\alpha ^{-1} + \sum _{t} \lambda _{it} \right)^{-\sum _{t} y_{it}} \end{eqnarray*}](images/etsug_countreg0321.png)
where 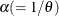 is the overdispersion parameter. This is the density of the Poisson random-effects model with gamma-distributed random effects.
For this distribution,
is the overdispersion parameter. This is the density of the Poisson random-effects model with gamma-distributed random effects.
For this distribution, 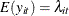 and
and 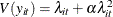 ; that is, there is overdispersion.
; that is, there is overdispersion.
Then the log-likelihood function is written as
![\begin{eqnarray*} \mathcal{L} & = & \sum _{i=1}^{N} \left\{ \sum _{t=1}^{T_{i}} \ln (\frac{\lambda _{it}^{y_{it}}}{y_{it}!}) + \alpha ^{-1} \ln (\alpha ^{-1}) -\alpha ^{-1} \ln (\alpha ^{-1}+\sum _{t=1}^{T_{i}}\lambda _{it}) \right\} \\ & & + \sum _{i=1}^{N} \left\{ - \left( \sum _{t=1}^{T_{i}}y_{it} \right) \ln \left(\alpha ^{-1}+\sum _{t=1}^{T_{i}}\lambda _{it}\right) \right. \\ & & \left. \; \; \; \; \; \; \; + \ln \left[\Gamma \left(\alpha ^{-1}+ \sum _{t=1}^{T_{i}}y_{it} \right)\right] -\ln (\Gamma (\alpha ^{-1})) \right\} \end{eqnarray*}](images/etsug_countreg0325.png)
The gradient is
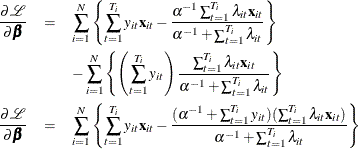
and
![\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial \alpha } & = & \sum _{i=1}^{N} \left\{ -\alpha ^{-2} \left[ [1+ \ln (\alpha ^{-1})] - \frac{(\alpha ^{-1}+\sum _{t=1}^{T_{i}} y_{it})}{(\alpha ^{-1})+ \sum _{t=1}^{T_{i}}\lambda _{it}} - \ln \left(\alpha ^{-1} + \sum _{t=1}^{T_{i}} \lambda _{it} \right) \right] \right\} \\ & + & \sum _{i=1}^{N} \left\{ -\alpha ^{-2} \left[ \frac{\Gamma '(\alpha ^{-1}+ \sum _{t=1}^{T_{i}} y_{it})}{\Gamma (\alpha ^{-1} +\sum _{t=1}^{T_{i}} y_{it})} -\frac{\Gamma '(\alpha ^{-1})}{\Gamma (\alpha ^{-1})} \right] \right\} \end{eqnarray*}](images/etsug_countreg0327.png)
where 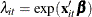 ,
, 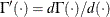 and
and 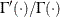 is the digamma function.
is the digamma function.
Panel Data Negative Binomial Regression with Fixed Effects
This section shows the derivation of a negative binomial model with fixed effects. Keep the assumptions of the Poisson-distributed dependent variable
![\[ y_{it}\sim Poisson\left(\mu _{it}\right) \]](images/etsug_countreg0331.png)
But now let the Poisson parameter be random with gamma distribution and parameters 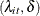 ,
,
![\[ \mu _{it}\sim \Gamma \left(\lambda _{it},\delta \right) \]](images/etsug_countreg0333.png)
where one of the parameters is the exponentially affine function of independent variables 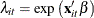 . Use integration by parts to obtain the distribution of
. Use integration by parts to obtain the distribution of 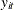 ,
,
![\begin{eqnarray*} P\left[y_{it}\right]& = & \int _{0}^{\infty }\frac{e^{-\mu _{it}}\mu _{it}^{y_{it}}}{y_{it}!}f\left(\mu _{it}\right)d\mu _{it}\\ & = & \frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}\left(\frac{\delta }{1+\delta }\right)^{\lambda _{it}}\left(\frac{1}{1+\delta }\right)^{y_{it}} \end{eqnarray*}](images/etsug_countreg0335.png)
which is a negative binomial distribution with parameters 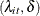 . Conditional joint distribution is given as
. Conditional joint distribution is given as
![\begin{eqnarray*} P[y_{i1},\ldots ,y_{iT_{i}}|\sum _{t=1}^{T_{i}}y_{it}]& =& \left(\prod _{t=1}^{T_{i}}\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}\right)\\ & & \times \left(\frac{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}\right)\Gamma \left(\sum _{t=1}^{T_{i}}y_{it}+1\right)}{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\right) \end{eqnarray*}](images/etsug_countreg0336.png)
Hence, the conditional fixed-effects negative binomial log-likelihood is
![\begin{eqnarray*} \mathcal{L}& = & \sum _{i=1}^{N}\left[\log \Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}\right)+\log \Gamma \left(\sum _{t=1}^{T_{i}}y_{it}+1\right)-\log \Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)\right]\\ & & +\sum _{i=1}^{N}\sum _{t=1}^{T_{i}}\left[\log \Gamma \left(\lambda _{it}+y_{it}\right)-\log \Gamma \left(\lambda _{it}\right)-\log \Gamma \left(y_{it}+1\right)\right] \end{eqnarray*}](images/etsug_countreg0337.png)
The gradient is
![\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial \beta }& = & \sum _{i=1}^{N}\left[\left(\frac{\Gamma '\left(\sum _{t=1}^{T_{i}}\lambda _{it}\right)}{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}\right)}-\frac{\Gamma '\left(\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\right)\sum _{t=1}^{T_{i}}\lambda _{it}\mathbf{x}_{it}\right]\\ & & +\sum _{i=1}^{N}\sum _{t=1}^{T_{i}}\left[\left(\frac{\Gamma '\left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}+y_{it}\right)}-\frac{\Gamma '\left(\lambda _{it}\right)}{\Gamma \left(\lambda _{it}\right)}\right)\lambda _{it}\mathbf{x}_{it}\right] \end{eqnarray*}](images/etsug_countreg0338.png)
Panel Data Negative Binomial Regression with Random Effects
This section describes the derivation of negative binomial model with random effects. Suppose
![\[ y_{it}\sim Poisson\left(\mu _{it}\right) \]](images/etsug_countreg0331.png)
with the Poisson parameter distributed as gamma,
![\[ \mu _{it}\sim \Gamma \left(\nu _{i}\lambda _{it},\delta \right) \]](images/etsug_countreg0339.png)
where its parameters are also random:
![\[ \nu _{i}\lambda _{it}=\exp \left(\mathbf{x}_{it}’\beta +\eta _{it}\right) \]](images/etsug_countreg0340.png)
Assume that the distribution of a function of 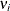 is beta with parameters
is beta with parameters 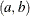 :
:
![\[ \frac{\nu _{i}}{1+\nu _{i}}\sim Beta\left(a,b\right) \]](images/etsug_countreg0343.png)
Explicitly, the beta density with ![$\left[0,1\right]$](images/etsug_countreg0344.png) domain is
domain is
![\[ f\left(z\right)=\left[B\left(a,b\right)\right]^{-1}z^{a-1}\left(1-z\right)^{b-1} \]](images/etsug_countreg0345.png)
where 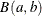 is the beta function. Then, conditional joint distribution of dependent variables is
is the beta function. Then, conditional joint distribution of dependent variables is
![\[ P[y_{i1},\ldots ,y_{iT_{i}}|\mathbf{x}_{i1},\ldots ,\mathbf{x}_{iT_{i}},\nu _{i}]=\prod _{t=1}^{T_{i}}\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}\left(\frac{1}{1+\nu _{i}}\right)^{\lambda _{it}}\left(\frac{\nu _{i}}{1+\nu _{i}}\right)^{y_{it}} \]](images/etsug_countreg0347.png)
Integrating out the variable 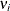 yields the following conditional distribution function:
yields the following conditional distribution function:
![\begin{eqnarray*} P[y_{i1},\ldots ,y_{iT_{i}}|\mathbf{x}_{i1},\ldots ,\mathbf{x}_{iT_{i}}]& = & \int _{0}^{1}\left[\prod _{t=1}^{T_{i}}\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}z_{i}^{\lambda _{it}}\left(1-z_{i}\right)^{y_{it}}\right]f\left(z_{i}\right)dz_{i}\\ & = & \frac{\Gamma \left(a+b\right)\Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)\Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(a\right)\Gamma \left(b\right)\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\\ & & \times \prod _{t=1}^{T_{i}}\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)} \end{eqnarray*}](images/etsug_countreg0348.png)
Consequently, the conditional log-likelihood function for a negative binomial model with random effects is
![\begin{eqnarray*} \mathcal{L}& = & \sum _{i=1}^{N}\left[\log \Gamma \left(a+b\right)+\log \Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)+\log \Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)\right]\\ & & -\sum _{i=1}^{N}\left[\log \Gamma \left(a\right)+\log \Gamma \left(b\right)+\log \Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)\right]\\ & & +\sum _{i=1}^{N}\sum _{t=1}^{T_{i}}\left[\log \Gamma \left(\lambda _{it}+y_{it}\right)-\log \Gamma \left(\lambda _{it}\right)-\log \Gamma \left(y_{it}+1\right)\right] \end{eqnarray*}](images/etsug_countreg0349.png)
The gradient is
![\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial \beta }& = & \sum _{i=1}^{N}\left[\frac{\Gamma '\left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)}{\Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)}\sum _{t=1}^{T_{i}}\lambda _{it}\mathbf{x}_{it}\right]\\ & & -\sum _{i=1}^{N}\left[\frac{\Gamma '\left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\sum _{t=1}^{T_{i}}\lambda _{it}\mathbf{x}_{it}\right]\\ & & +\sum _{i=1}^{N}\sum _{t=1}^{T_{i}}\left[\left(\frac{\Gamma '\left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}+y_{it}\right)}-\frac{\Gamma '\left(\lambda _{it}\right)}{\Gamma \left(\lambda _{it}\right)}\right)\lambda _{it}\mathbf{x}_{it}\right] \end{eqnarray*}](images/etsug_countreg0350.png)
and
![\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial a}& = & \sum _{i=1}^{N}\left[\frac{\Gamma '\left(a+b\right)}{\Gamma \left(a+b\right)}+\frac{\Gamma '\left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)}{\Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)}\right]\\ & & -\sum _{i=1}^{N}\left[\frac{\Gamma '\left(a\right)}{\Gamma \left(a\right)}+\frac{\Gamma '\left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\right] \end{eqnarray*}](images/etsug_countreg0351.png)
and
![\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial b}& = & \sum _{i=1}^{N}\left[\frac{\Gamma '\left(a+b\right)}{\Gamma \left(a+b\right)}+\frac{\Gamma '\left(b+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)}\right]\\ & & -\sum _{i=1}^{N}\left[\frac{\Gamma '\left(b\right)}{\Gamma \left(b\right)}+\frac{\Gamma '\left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\right] \end{eqnarray*}](images/etsug_countreg0352.png)