The COUNTREG Procedure
- Overview
- Getting Started
-
Syntax
 Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSPATIALDISPEFFECTS StatementSPATIALEFFECTS StatementSPATIALID StatementSPATIALZEROEFFECTS StatementSTORE StatementTEST StatementWEIGHT StatementZEROMODEL Statement
Functional SummaryPROC COUNTREG StatementBAYES StatementBOUNDS StatementBY StatementCLASS StatementDISPMODEL StatementFREQ StatementINIT StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPERFORMANCE StatementPRIOR StatementRESTRICT StatementSCORE StatementSHOW StatementSPATIALDISPEFFECTS StatementSPATIALEFFECTS StatementSPATIALID StatementSPATIALZEROEFFECTS StatementSTORE StatementTEST StatementWEIGHT StatementZEROMODEL Statement -
Details
 Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionSpatial Lag of X ModelVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreParameter Naming Conventions for the RESTRICT, TEST, BOUNDS, and INIT StatementsComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmMarginal LikelihoodOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics
Specification of RegressorsMissing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionSpatial Lag of X ModelVariable SelectionPanel Data AnalysisBY Groups and Scoring with an Item StoreParameter Naming Conventions for the RESTRICT, TEST, BOUNDS, and INIT StatementsComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputBayesian AnalysisPrior DistributionsAutomated MCMC AlgorithmMarginal LikelihoodOUTPUT OUT= Data SetOUTEST= Data SetODS Table NamesODS Graphics -
Examples

- References
Zero-Inflated Poisson Regression
In the zero-inflated Poisson (ZIP) regression model, the data generation process that is referred to earlier as Process 2 is
![\[ g(y_{i}) = \frac{\exp (-\mu _{i})\mu _{i}^{y_{i}}}{y_{i}!} \]](images/etsug_countreg0199.png)
where 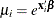 . Thus the ZIP model is defined as
. Thus the ZIP model is defined as
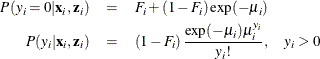
The conditional expectation and conditional variance of 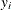 are given by
are given by
![\[ E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = \mu _{i}(1 -F_{i}) \]](images/etsug_countreg0202.png)
![\[ V(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i})(1+\mu _{i}F_{i}) \]](images/etsug_countreg0203.png)
Note that the ZIP model (as well as the ZINB model) exhibits overdispersion because 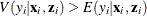 .
.
In general, the log-likelihood function of the ZIP model is
![\[ \mathcal{L} = \sum _{i=1}^{N}w_ i\ln \left[ P(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) \right] \]](images/etsug_countreg0205.png)
After a specific link function (either logistic or standard normal) for the probability 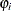 is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.
is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.
ZIP Model with Logistic Link Function
First, consider the ZIP model in which the probability 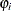 is expressed using a logistic link function—namely,
is expressed using a logistic link function—namely,
![\[ \varphi _{i}=\frac{\exp (\mathbf{z}_{i}'\bgamma )}{1+\exp (\mathbf{z}_{i}'\bgamma )} \]](images/etsug_countreg0206.png)
The log-likelihood function is
![\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} } w_ i\ln \left[\exp (\mathbf{z}_{i}’\bgamma )+\exp (-\exp (\mathbf{x}_{i}’\bbeta )) \right] \\ & & + \sum _{\{ i: y_{i}>0\} }w_ i\left[y_{i} \mathbf{x}_{i}’\bbeta -\exp (\mathbf{x}_{i}’\bbeta ) - \sum _{k=2}^{y_{i}}\ln (k) \right] \\ & & - \sum _{i=1}^{N}w_ i\ln \left[ 1 + \exp (\mathbf{z}_{i}’\bgamma ) \right] \end{eqnarray*}](images/etsug_countreg0207.png)
See the section Poisson Regression for the definition of 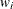 .
.
The gradient for this model is given by
![\[ \frac{\partial \mathcal{L}}{\partial \bgamma } = \sum _{\{ i: y_{i}=0\} } w_ i\left[\frac{\exp (\mathbf{z}_{i}'\bgamma )}{\exp (\mathbf{z}_{i}'\bgamma ) + \exp (-\exp (\mathbf{x}_{i}'\bbeta ))}\right] \mathbf{z}_{i} - \sum _{i=1}^{N}w_ i\left[\frac{\exp (\mathbf{z}_{i}'\bgamma )}{1 + \exp (\mathbf{z}_{i}'\bgamma )} \right] \mathbf{z}_{i} \]](images/etsug_countreg0208.png)
![\[ \frac{\partial \mathcal{L}}{\partial \bbeta } = \sum _{\{ i: y_{i}=0\} } w_ i\left[\frac{-\exp (\mathbf{x}_{i}'\bbeta ) \exp (-\exp (\mathbf{x}_{i}'\bbeta ))}{\exp (\mathbf{z}_{i}'\bgamma ) + \exp (-\exp (\mathbf{x}_{i}'\bbeta ))}\right] \mathbf{x}_{i} + \sum _{\{ i: y_{i}>0\} }w_ i\left[y_{i} - \exp (\mathbf{x}_{i}’\bbeta ) \right] \mathbf{x}_{i} \]](images/etsug_countreg0209.png)
ZIP Model with Standard Normal Link Function
Next, consider the ZIP model in which the probability 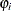 is expressed using a standard normal link function:
is expressed using a standard normal link function: 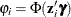 . The log-likelihood function is
. The log-likelihood function is
![\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} }w_ i\ln \left\{ \Phi (\mathbf{z}_{i}’\bgamma ) + \left[ 1- \Phi (\mathbf{z}_{i}’\bgamma )\right] \exp (-\exp (\mathbf{x}_{i}’\bbeta )) \right\} \\ & + & \sum _{\{ i: y_{i}>0\} }w_ i\left\{ \ln \left[ \left( 1-\Phi (\mathbf{z}_{i}’\bgamma )\right) \right] - \exp (\mathbf{x}_{i}’\bbeta ) + y_{i} \mathbf{x}_{i}’\bbeta - \sum _{k=2}^{y_{i}} \ln (k) \right\} \end{eqnarray*}](images/etsug_countreg0211.png)
See the section Poisson Regression for the definition of 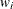 .
.
The gradient for this model is given by
![\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial \bgamma } & = & \sum _{\{ i: y_{i}=0\} } w_ i\frac{\varphi (\mathbf{z}_{i}'\bgamma )\left[ 1-\exp (-\exp (\mathbf{x}_{i}'\bbeta )) \right]}{\Phi (\mathbf{z}_{i}'\bgamma ) + \left[ 1 - \Phi (\mathbf{z}_{i}'\bgamma ) \right] \exp (-\exp (\mathbf{x}_{i}'\bbeta ))} \mathbf{z}_{i} \\ & - & \sum _{\{ i: y_{i}>0\} } w_ i\frac{\varphi (\mathbf{z}_{i}'\bgamma )}{\left[ 1 - \Phi (\mathbf{z}_{i}'\bgamma ) \right]} \mathbf{z}_{i} \end{eqnarray*}](images/etsug_countreg0212.png)
![\begin{eqnarray*} \frac{\partial \mathcal{L}}{\partial \bbeta } & = & \sum _{\{ i: y_{i}=0\} } w_ i\frac{-\left[1-\Phi (\mathbf{z}_{i}'\bgamma )\right] \exp (\mathbf{x}_{i}'\bbeta ) \exp (-\exp (\mathbf{x}_{i}'\bbeta ))}{\Phi (\mathbf{z}_{i}'\bgamma ) + \left[ 1 - \Phi (\mathbf{z}_{i}'\bgamma ) \right] \exp (-\exp (\mathbf{x}_{i}'\bbeta ))} \mathbf{x}_{i} \\ & + & \sum _{\{ i: y_{i}>0\} } w_ i\left[y_{i}-\exp (\mathbf{x}_{i}’\bbeta ) \right] \mathbf{x}_{i} \end{eqnarray*}](images/etsug_countreg0213.png)