The UCM Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC UCM StatementAUTOREG StatementBLOCKSEASON StatementBY StatementCYCLE StatementDEPLAG StatementESTIMATE StatementFORECAST StatementID StatementIRREGULAR StatementLEVEL StatementMODEL StatementNLOPTIONS StatementOUTLIER StatementPERFORMANCE StatementRANDOMREG StatementSEASON StatementSLOPE StatementSPLINEREG StatementSPLINESEASON Statement
Functional SummaryPROC UCM StatementAUTOREG StatementBLOCKSEASON StatementBY StatementCYCLE StatementDEPLAG StatementESTIMATE StatementFORECAST StatementID StatementIRREGULAR StatementLEVEL StatementMODEL StatementNLOPTIONS StatementOUTLIER StatementPERFORMANCE StatementRANDOMREG StatementSEASON StatementSLOPE StatementSPLINEREG StatementSPLINESEASON Statement -
Details

-
Examples

- References
In April 1979 the Albuquerque Police Department began a special enforcement program aimed at reducing the number of DWI (driving while intoxicated) accidents. The program was administered by a squad of police officers, who used breath alcohol testing (BAT) devices and a van that houses a BAT device (Batmobile). These data were collected by the Division of Governmental Research of the University of New Mexico, under a contract with the National Highway Traffic Safety Administration of the U.S. Department of Transportation, to evaluate the Batmobile program. The first 29 observations are for a control period, and the next 23 observations are for the experimental (Batmobile) period. The data, freely available at http://lib.stat.cmu.edu/DASL/Datafiles/batdat.html, consist of two variables: ACC, which represents injuries and fatalities from Wednesday to Saturday nighttime accidents, and FUEL, which represents fuel consumption (millions of gallons) in Albuquerque. The variables are measured quarterly starting from the first quarter of 1972 up to the last quarter of 1984, covering the span of 13 years. The following DATA step statements create the input data set.
data bat; input ACC FUEL @@; batProgram = 0; if _n_ > 29 then batProgram = 1; date = INTNX( 'qtr', '1jan1972'd, _n_- 1 ); format date qtr8.; datalines; 192 32.592 238 37.250 232 40.032 246 35.852 185 38.226 274 38.711 266 43.139 196 40.434 170 35.898 234 37.111 272 38.944 234 37.717 210 37.861 280 42.524 246 43.965 248 41.976 269 42.918 326 49.789 342 48.454 257 45.056 280 49.385 290 42.524 356 51.224 295 48.562 279 48.167 330 51.362 354 54.646 331 53.398 291 50.584 377 51.320 327 50.810 301 46.272 269 48.664 314 48.122 318 47.483 288 44.732 242 46.143 268 44.129 327 46.258 253 48.230 215 46.459 263 50.686 319 49.681 263 51.029 206 47.236 286 51.717 323 51.824 306 49.380 230 47.961 304 46.039 311 55.683 292 52.263 ;
There are a number of ways to study these data and the question of the effectiveness of the BAT program. One possibility is to study the before-after difference in the injuries and fatalities per million gallons of fuel consumed, by regressing ACC on the FUEL and the dummy variable BATPROGRAM, which is zero before the program began and one while the program is in place. However, it is possible that the effect of the Batmobiles might well be cumulative, because as awareness of the program becomes dispersed, its effectiveness as a deterrent to driving while intoxicated increases. This suggests that the regression coefficient of the BATPROGRAM variable might be time varying. The following program fits a model that incorporates these considerations. A seasonal component is included in the model since it is easy to see that the data show strong quarterly seasonality.
proc ucm data=bat; model acc = fuel; id date interval=qtr; irregular; level var=0 noest; randomreg batProgram / plot=smooth; season length=4 var=0 noest plot=smooth; estimate plot=(panel residual); forecast plot=forecasts lead=0; run;
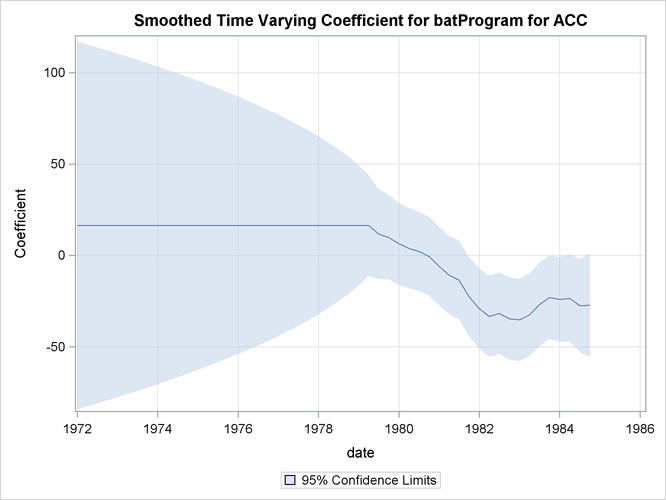
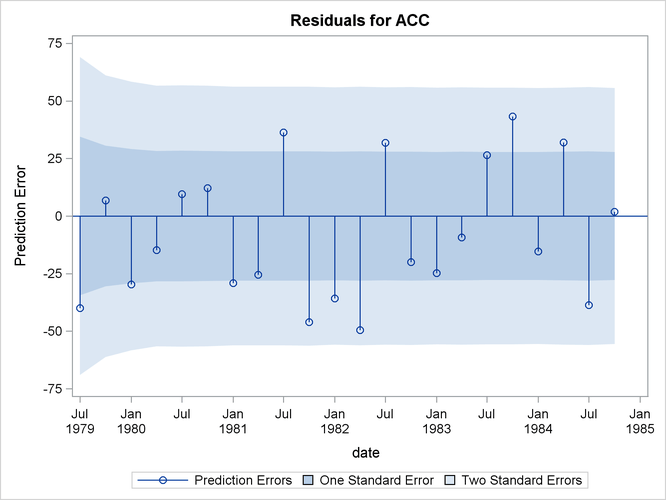
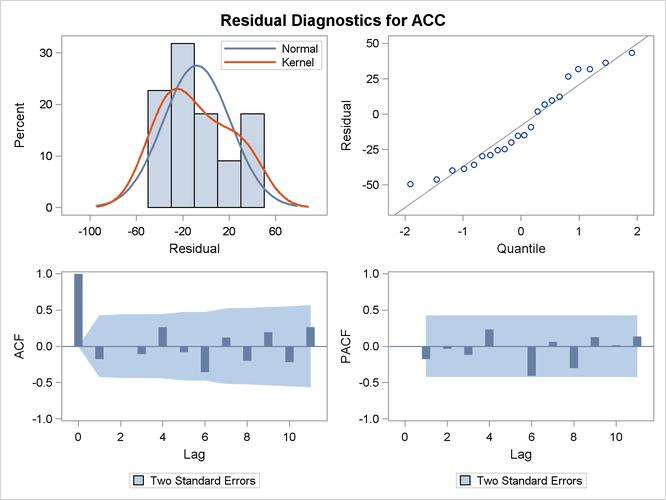
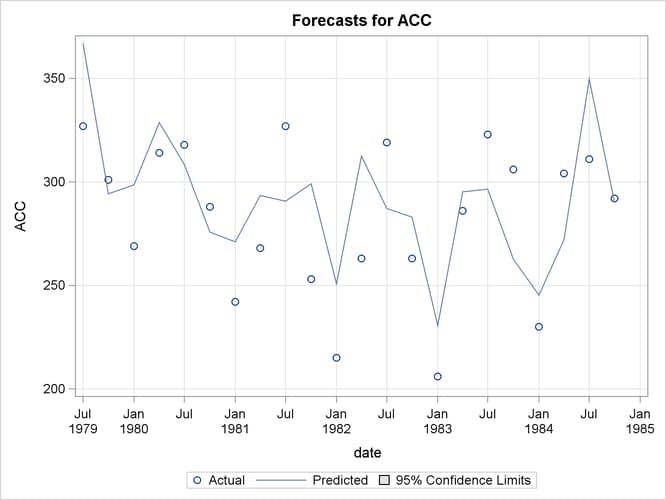
The model seems to fit the data adequately. No data are withheld for model validation because the series is relatively short. The plot of the time-varying coefficient of BATPROGRAM is shown in Output 34.4.1. As expected, it shows that the effectiveness of the program increases as awareness of the program becomes dispersed. The effectiveness eventually seems to level off. The residual diagnostic plots are shown in Output 34.4.2 and Output 34.4.3, the forecast plot is in Output 34.4.4, the goodness-of-fit statistics are in Output 34.4.5, and the parameter estimates are in Output 34.4.6.
Output 34.4.5: Model Fit for the Time-Varying Regression Model
| Fit Statistics Based on Residuals | |
|---|---|
| Mean Squared Error | 866.75562 |
| Root Mean Squared Error | 29.44071 |
| Mean Absolute Percentage Error | 9.50326 |
| Maximum Percent Error | 14.15368 |
| R-Square | 0.32646 |
| Adjusted R-Square | 0.29278 |
| Random Walk R-Square | 0.63010 |
| Amemiya's Adjusted R-Square | 0.19175 |
| Number of non-missing residuals used for computing the fit statistics = 22 | |