The COPULA Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasHierarchical Archimedean Copula (HAC)Canonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names
Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasHierarchical Archimedean Copula (HAC)Canonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names -
Examples

- References
There are three basic types of measures: linear correlation, rank correlation, and tail dependence. Linear correlation is given by
The linear correlation coefficient carries very limited information about the joint properties of the variables. A well-known property is that uncorrelatedness does not imply independence, while independence implies noncorrelation. In addition, there exist distinct bivariate distributions that have the same marginal distribution and the same correlation coefficient. These results suggest that caution must be used when interpreting the linear correlation.
Another statistical measure of dependence is called rank correlation, which is nonparametric. Kendall’s tau, for example,
is the covariance between the sign statistic ![]() and
and ![]() , where
, where ![]() is an independent copy of
is an independent copy of ![]() :
:
The sign function (sometimes written as sgn) is defined by
![\[ \textrm{sign}(x)= \begin{cases} -1 & \mr{if } x \le 0 \\ 0 & \mr{if } x = 0 \\ 1 & \mr{if } x \ge 0 \end{cases} \]](images/etsug_copula0025.png)
Spearman’s rho is the correlation between the transformed random variables:
The variables are transformed by their distribution functions so that the transformed variables are uniformly distributed
on ![]() . The rank correlations depend only on the copula of the random variables and are indifferent to the marginal distributions.
Like linear correlation, the rank correlations have their limitations. In particular, there are different copulas that result
in the same rank correlation.
. The rank correlations depend only on the copula of the random variables and are indifferent to the marginal distributions.
Like linear correlation, the rank correlations have their limitations. In particular, there are different copulas that result
in the same rank correlation.
A third measure focuses on only part of the joint properties between the variables. Tail dependence measures the dependence when both variables are at extreme values. Formally, they can be defined as the conditional probabilities of quantile exceedances. There are two types of tail dependence:
-
The upper tail dependence, denoted
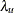 , is
, is
![\[ \lambda _ u(X_1,X_2) \equiv \lim _{q->1^-} P(X_2> F_2^{-1}(q)|X_1>F_1^{-1}(q)) \]](images/etsug_copula0029.png)
when the limit exists
![$\lambda _ u \in [0,1]$](images/etsug_copula0030.png) . Here
. Here 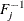 is the quantile function (that is, the inverse of the CDF).
is the quantile function (that is, the inverse of the CDF).
-
The lower tail dependence is defined symmetrically.
Tail dependence is hard to detect by looking at a scatter plot of realizations of two random variables. One graphical way
to detect tail dependence between two variables is by creating the chi plot of those two variables. The chi plot, as defined
in Fisher and Switzer (2001), has characteristic patterns that depend on the dependence structure between the variables. The chi plot for the random
variables ![]() and
and ![]() is a scatter plot of the pairs
is a scatter plot of the pairs ![]() for each data point
for each data point ![]() .
. ![]() is a measure of the distance of the data point
is a measure of the distance of the data point ![]() from the center of the data as measured by the median values of
from the center of the data as measured by the median values of ![]() , and
, and ![]() is a correlation coefficient between dichotomized values of
is a correlation coefficient between dichotomized values of ![]() and
and ![]() . A positive
. A positive ![]() means that
means that ![]() and
and ![]() are either both large with respect to their median values or both small. A negative
are either both large with respect to their median values or both small. A negative ![]() means that
means that ![]() or
or ![]() is large with respect to its median, whereas the other value is small. Signs of tail dependence manifest as clusters of points
that are significantly far from the
is large with respect to its median, whereas the other value is small. Signs of tail dependence manifest as clusters of points
that are significantly far from the ![]() axis around
axis around ![]() values of
values of ![]() 1. If
1. If ![]() and
and ![]() are uncorrelated, the
are uncorrelated, the ![]() values cluster around the
values cluster around the ![]() axis.
axis.