The COPULA Procedure

Sklar’s Theorem

The copula models are tools for studying the dependence structure of multivariate distributions. The usual joint distribution function contains the information both about the marginal behavior of the individual random variables and about the dependence structure between the variables. The copula is introduced to decouple the marginal properties of the random variables and the dependence structures. A m-dimensional copula is a joint distribution function on $[0,1]^ m$ with all marginal distributions being standard uniform. The common notation for a copula is $C(u_1,\ldots ,u_ m)$ .

The Sklar (1959) theorem shows the importance of copulas in modeling multivariate distributions. The first part claims that a copula can be derived from any joint distribution functions, and the second part asserts the opposite: that is, any copula can be combined with any set of marginal distributions to result in a multivariate distribution function.

Let 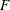$F$ be a joint distribution function and 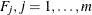$F_ j,j=1,\ldots ,m$ be the marginal distributions. Then there exists a copula $C: [0,1]^ m \rightarrow [0,1]$ such that

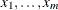$F(x_1,\ldots ,x_ m)= C(F_1(x_1),\ldots ,F_ m(x_ m))$

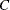for all $x_1,\ldots ,x_ m$ in $[-\infty ,\infty ]$ . Moreover, if the margins are continuous, then $C$ is unique; otherwise 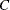$C$ is uniquely determined on 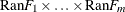$\textrm{Ran}F_1 \times \ldots \times \textrm{Ran}F_ m$ , where $\textrm{Ran}F_ j =F_ j([-\infty ,\infty ])$ is the range of $F_ j$ .
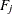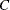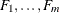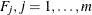The converse is also true. That is, if $C$ is a copula and $F_1,\ldots ,F_ m$ are univariate distribution functions, then the multivariate function defined in the preceding equation is a joint distribution function with marginal distributions $F_ j,j=1,\ldots ,m$ .