VARMA and VARMAX Modeling
Previous Page|Next Page

The VARMAX Procedure

VARMA and VARMAX Modeling

Subsections:

A zero-mean VARMA($p,q$) process is written as

\begin{eqnarray*} \mb {y} _{t} = \sum _{i=1}^{p}\Phi _ i\mb {y} _{t-i} + \bepsilon _ t -\sum _{i=1}^{q} \Theta _ i\bepsilon _{t-i} \end{eqnarray*}

or

\begin{eqnarray*} \Phi (B) \mb {y} _{t} = \Theta (B) \bepsilon _ t \end{eqnarray*}

where $\Phi (B) = I_ k - \sum _{i=1}^{p} \Phi _ i B^ i$ and $\Theta (B) = I_ k - \sum _{i=1}^{q} \Theta _ i B^ i$.

Stationarity and Invertibility

For stationarity and invertibility of the VARMA process, the roots of $|\Phi (z)|=0$ and $|\Theta (z)|=0$ are outside the unit circle.

Parameter Estimation

Under the assumption of normality of the $\bepsilon _{t}$ with zero mean vector and nonsingular covariance matrix $\Sigma $, the conditional (approximate) log-likelihood function of a zero-mean VARMA($p$,$q$) model is considered.

Define $Y=(\mb {y} _{1},\ldots ,\mb {y} _{T})’$ and $E=(\bepsilon _{1},\ldots ,\bepsilon _{T})’$ with $B^ i Y=(\mb {y} _{1-i},\ldots ,\mb {y} _{T-i})’$ and $B^ i E=(\bepsilon _{1-i},\ldots ,\bepsilon _{T-i})’$; define $\mb {y} =\mr {vec} (Y’)$ and $\mb {e} =\mr {vec} (E’)$. Then

\[ \mb {y} -\sum _{i=1}^ p (I_ T \otimes \Phi _ i)B^ i \mb {y} =\mb {e} - \sum _{i=1}^ q (I_ T \otimes \Theta _ i)B^ i \mb {e} \]

where $B^ i \mb {y} = \mr {vec} [(B^ i Y)’]$ and $B^ i \mb {e} = \mr {vec} [(B^ i E)’]$.

Then, the conditional (approximate) log-likelihood function can be written as follows (Reinsel, 1997):

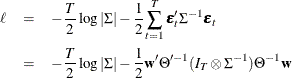
\begin{eqnarray*} \ell & =& -\frac{T}{2} \log |\Sigma | -\frac{1}{2}\sum _{t=1}^ T \bepsilon _{t}’\Sigma ^{-1}\bepsilon _{t} \\ & =& -\frac{T}{2} \log |\Sigma |-\frac{1}{2}\mb {w} ’\Theta ’^{-1} (I_ T\otimes \Sigma ^{-1})\Theta ^{-1}\mb {w} \end{eqnarray*}

where $\mb {w} = \mb {y} -\sum _{i=1}^ p (I_ T \otimes \Phi _ i)B^ i \mb {y}$, and $\Theta $ is such that $\mb {e} -\sum _{i=1}^ q(I_ T\otimes \Theta _ i)B^ i\mb {e} =\Theta \mb {e}$.

For the exact log-likelihood function of a VARMA($p$,$q$) model, the Kalman filtering method is used for transforming the VARMA process into the state-space form (Reinsel, 1997).

The state-space form of the zero-mean VARMA($p$,$q$) model consists of a state equation

\[ \mb {z} _{t} =F\mb {z} _{t-1} + G\bepsilon _{t} \]

and an observation equation

\[ \mb {y} _ t = H\mb {z} _{t} \]

where for $v=\mr {max} (p,q+1)$

\[ \mb {z} _{t}=(\mb {y} _{t}’,\mb {y} _{t+1|t}’,\ldots ,\mb {y} _{t+v-1|t}’)’ \]
\[ F = \left[\begin{matrix} 0 & I_ k & 0 & {\cdots } & 0 \\ 0 & 0 & I_ k & {\cdots } & 0 \\ {\vdots } & {\vdots } & {\vdots } & \ddots & {\vdots } \\ \Phi _{v} & \Phi _{v-1} & \Phi _{v-2} & {\cdots } & \Phi _{1} \\ \end{matrix} \right], ~ ~ G = \left[\begin{matrix} I_ k \\ \Psi _{1} \\ {\vdots } \\ \Psi _{v-1} \\ \end{matrix}\right] \]

and

\[ H = [I_ k, 0, \ldots , 0] \]

The Kalman filtering approach is used for evaluation of the likelihood function. The updating equation is

\[ \hat{\mb {z}}_{t|t} = {\hat{\mb {z}}}_{t|t-1} + K_ t\bepsilon _{t|t-1} \]

where

\[ K_ t = P_{t|t-1}H’[H P_{t|t-1} H’]^{-1} \]

The prediction equation is

\[ \hat{\mb {z} }_{t|t-1} = F \hat{\mb {z} }_{t-1|t-1}, ~ ~ P_{t|t-1} = F P_{t-1|t-1} F’ + G \Sigma G’ \]

where $P_{t|t} = [I-K_ tH]P_{t|t-1}$ for $t=1,2,\ldots ,n$.

The log-likelihood function can be expressed as

\[ \ell = -\frac{1}{2} \sum _{t=1}^ T [ \log |\Sigma _{t|t-1}| + (\mb {y} _{t}-\hat{\mb {y} }_{t|t-1})’\Sigma _{t|t-1}^{-1} (\mb {y} _{t}-\hat{\mb {y} }_{t|t-1}) ] \]

where $\hat{\mb {y} }_{t|t-1}$ and $\Sigma _{t|t-1}$ are determined recursively from the Kalman filter procedure. To construct the likelihood function from Kalman filtering, you obtain $\hat{\mb {y} }_{t|t-1}=H \hat{\mb {z} }_{t|t-1}$, $\hat{\bepsilon }_{t|t-1} = \mb {y} _{t}-\hat{\mb {y} }_{t|t-1}$, and $\Sigma _{t|t-1}=H P_{t|t-1} H’$.

Define the vector $\bbeta $ as

\[ \bbeta = ( \phi _1’, \ldots , \phi _ p’, \theta _1’, \ldots , \theta _ q’, \mr {vech} (\Sigma ) )’ \]

where $\phi _ i=\mr {vec} (\Phi _ i)$ and $\theta _ i=\mr {vec} (\Theta _ i)$. All elements of $\bbeta $ are estimated through the preceding maximum likelihood method. The estimates of $\Phi _ i, i=1, ..., p$ and $\Theta _ i, i=1, ..., q$ are output in the ParameterEstimates ODS table. The estimates of the covariance matrix ($\Sigma $) are output in the CovarianceParameterEstimates ODS table. If you specify the OUTEST=, OUTCOV, PRINT=(COVB), or PRINT=(CORRB) option, you can see all elements of $\bbeta $, including the covariance matrix $\Sigma $, in the parameter estimates, covariance of parameter estimates, or correlation of parameter estimates. You can also apply the BOUND, INITIAL, RESTRICT, and TEST statements to any elements of $\bbeta $, including the covariance matrix $\Sigma $. For more information, see the syntax of the corresponding statement.

The log-likelihood equations are solved by iterative numerical procedures such as quasi-Newton optimization. The starting values for the AR and MA parameters are obtained from the least squares estimates.

Asymptotic Distribution of the Parameter Estimates

Under the assumptions of stationarity and invertibility for the VARMA model and the assumption that $\bepsilon _{t}$ is a white noise process, $\hat{\bbeta }$ is a consistent estimator for ${\bbeta }$ and $\sqrt {T}(\hat{\bbeta } - {\bbeta })$ converges in distribution to the multivariate normal $N(0, V^{-1})$ as $T \rightarrow \infty $, where $V$ is the asymptotic information matrix of ${\bbeta }$.

Asymptotic Distributions of Impulse Response Functions

Defining the vector $\bbeta $

\[ \bbeta = ( \phi _1’, \ldots , \phi _ p’, \theta _1’, \ldots , \theta _ q’ )’ \]

the asymptotic distribution of the impulse response function for a VARMA($p,q$) model is

\[ \sqrt {T} \mr {vec} (\hat\Psi _ j - \Psi _ j ) \stackrel{d}{\rightarrow } N(0, G_ j\Sigma _{\bbeta } G_ j’) ~ ~ j=1,2,\ldots \]

where $\Sigma _{\bbeta }$ is the covariance matrix of the parameter estimates and

\[ G_ j= \frac{\partial \mr {vec} (\Psi _ j)}{\partial {\bbeta }} = \sum _{i=0}^{j-1} \mb {H} ’(\mb {A} ’)^{j-1-i} \otimes \mb {J} \mb {A} ^ i\mb {J} ’ \]

where $\mb {H} = [ I_ k, 0,\ldots , 0, I_ k, 0,\ldots , 0]’$ is a $k(p+q)\times k$ matrix with the second $I_ k$ following after $p$ block matrices; $\mb {J} = [ I_ k, 0,\ldots , 0 ]$ is a $k\times k(p+q)$ matrix; $\mb {A} $ is a $k(p+q)\times k(p+q)$ matrix,

\begin{eqnarray*} \mb {A} = \left[\begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{matrix}\right] \end{eqnarray*}

where

\begin{eqnarray*} A_{11} = \left[ \begin{matrix} \Phi _1 & \Phi _2 & \cdots & \Phi _{p-1} & \Phi _{p} \\ I_ k & 0 & \cdots & 0 & 0 \\ 0 & I_ k & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & I_ k & 0 \\ \end{matrix} \right] ~ ~ A_{12} = \left[ \begin{matrix} -\Theta _1 & \cdots & -\Theta _{q-1} & -\Theta _{q} \\ 0 & \cdots & 0 & 0 \\ 0 & \cdots & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & 0 & 0 \\ \end{matrix} \right] \end{eqnarray*}

    $ A_{21}$ is a $kq\times kp$ zero matrix, and

\begin{eqnarray*} A_{22} = \left[ \begin{matrix} 0 & 0 & \cdots & 0 & 0 \\ I_ k & 0 & \cdots & 0 & 0 \\ 0 & I_ k & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & I_ k & 0 \\ \end{matrix} \right] \end{eqnarray*}

An Example of a VARMA(1,1) Model

Consider a VARMA(1,1) model with mean zero,

\begin{eqnarray*} \mb {y} _{t} = \Phi _1\mb {y} _{t-1} + \bepsilon _ t - \Theta _1\bepsilon _{t-1} \end{eqnarray*}

where $\bepsilon _ t$ is the white noise process with a mean zero vector and the positive-definite covariance matrix $\Sigma $.

The following IML procedure statements simulate a bivariate vector time series from this model to provide test data for the VARMAX procedure: 

proc iml;
   sig = {1.0  0.5, 0.5 1.25};
   phi = {1.2 -0.5, 0.6 0.3};
   theta = {0.5 -0.2, 0.1 0.3};
   /* to simulate the vector time series */
   call varmasim(y,phi,theta) sigma=sig n=100 seed=34657;
   cn = {'y1' 'y2'};
   create simul3 from y[colname=cn];
   append from y;
run;

The following statements fit a VARMA(1,1) model to the simulated data. You specify the order of the autoregressive model by using the P= option and specify the order of moving-average model by using the Q= option. You specify the quasi-Newton optimization in the NLOPTIONS statement as an optimization method. 

proc varmax data=simul3;
   nloptions tech=qn;
   model y1 y2 / p=1 q=1 noint print=(estimates);
run;

Figure 35.46 shows the initial values of parameters. The initial values were estimated by using the least squares method.

Figure 35.46: Start Parameter Estimates for the VARMA(1, 1) Model

The VARMAX Procedure

Optimization Start
Parameter Estimates
N Parameter Estimate Gradient
Objective
Function
1 AR1_1_1 1.013118 -0.897170
2 AR1_2_1 0.510233 0.262244
3 AR1_1_2 -0.399051 0.640577
4 AR1_2_2 0.441344 -8.443760
5 MA1_1_1 0.295872 -1.805699
6 MA1_2_1 -0.002809 2.098520
7 MA1_1_2 -0.044216 -0.575174
8 MA1_2_2 0.425334 0.791139
9 COV1_1 1.330160 2.522806
10 COV1_2 0.407148 -2.343560
11 COV2_2 1.491404 3.948366


Figure 35.47 shows the default option settings for the quasi-Newton optimization technique.

Figure 35.47: Default Criteria for the quasi-Newton Optimization

Minimum Iterations 0
Maximum Iterations 200
Maximum Function Calls 2000
ABSGCONV Gradient Criterion 0.00001
GCONV Gradient Criterion 1E-8
ABSFCONV Function Criterion 0
FCONV Function Criterion 2.220446E-16
FCONV2 Function Criterion 0
FSIZE Parameter 0
ABSXCONV Parameter Change Criterion 0
XCONV Parameter Change Criterion 0
XSIZE Parameter 0
ABSCONV Function Criterion -1.34078E154
Line Search Method 2
Starting Alpha for Line Search 1
Line Search Precision LSPRECISION 0.4
DAMPSTEP Parameter for Line Search .
Singularity Tolerance (SINGULAR) 1E-8


Figure 35.48 shows the iteration history of parameter estimates.

Figure 35.48: Iteration History of Parameter Estimates

Iteration   Restarts Function
Calls 		Active
Constraints 		  Objective
Function 		Objective
Function
Change 		Max Abs
Gradient
Element 		Step
Size 		Slope of
Search
Direction
1   0 5 0   122.10816 0.1580 7.2509 0.00486 -64.337
2   0 7 0   121.88166 0.2265 4.9540 1.000 -0.340
3   0 9 0   121.62016 0.2615 4.5335 1.000 -0.383
4   0 11 0   121.44241 0.1777 3.7692 1.000 -0.260
5   0 15 0   121.27005 0.1724 4.7159 2.000 -0.189
6   0 17 0   121.12987 0.1402 5.3950 2.668 -0.162
7   0 20 0   121.07909 0.0508 1.9377 1.045 -0.0872
8   0 23 0   121.06293 0.0162 1.1396 1.347 -0.0235
9   0 26 0   121.05350 0.00943 0.7476 1.739 -0.0109
10   0 28 0   121.04733 0.00617 1.3794 5.300 -0.0044
11   0 30 0   121.03785 0.00948 0.3432 1.248 -0.0124
12   0 33 0   121.03607 0.00178 0.2326 1.260 -0.0028
13   0 36 0   121.03566 0.000417 0.1110 2.521 -0.0003
14   0 39 0   121.03540 0.000258 0.0747 2.677 -0.0002
15   0 42 0   121.03525 0.000144 0.0815 3.525 -0.0001
16   0 45 0   121.03521 0.000041 0.0703 2.322 -35E-6
17   0 47 0   121.03519 0.000026 0.0445 3.340 -304E-7
18   0 50 0   121.03518 8.928E-6 0.00645 1.008 -177E-7
19   0 52 0   121.03518 5.534E-7 0.0129 10.000 -165E-9


Figure 35.49 shows the final parameter estimates.

Figure 35.49: Results of Parameter Estimates for the VARMA(1, 1) Model

The VARMAX Procedure

Optimization Results
Parameter Estimates
N Parameter Estimate Gradient
Objective
Function
1 AR1_1_1 1.018458 -0.010483
2 AR1_2_1 0.391825 0.012937
3 AR1_1_2 -0.386819 -0.009399
4 AR1_2_2 0.552806 0.011177
5 MA1_1_1 0.322920 0.003909
6 MA1_2_1 -0.165007 -0.004186
7 MA1_1_2 -0.021595 0.002849
8 MA1_2_2 0.585758 -0.003038
9 COV1_1 1.252015 0.000974
10 COV1_2 0.379502 -0.002960
11 COV2_2 1.313151 0.001441


Figure 35.50 shows the AR coefficient matrix in terms of lag 1, the MA coefficient matrix in terms of lag 1, the parameter estimates, and their significance, which is one indication of how well the model fits the data.

Figure 35.50: Parameter Estimates for the VARMA(1, 1) Model

The VARMAX Procedure

Type of Model VARMA(1,1)
Estimation Method Maximum Likelihood Estimation

AR
Lag Variable y1 y2
1 y1 1.01846 -0.38682
  y2 0.39182 0.55281

MA
Lag Variable e1 e2
1 y1 0.32292 -0.02160
  y2 -0.16501 0.58576

Schematic Representation
Variable/Lag AR1 MA1
y1 +- +.
y2 ++ .+
+ is > 2*std error,  - is < -2*std error,  . is between,  * is N/A

Model Parameter Estimates
Equation Parameter Estimate Standard
Error 		t Value Pr > |t| Variable
y1 AR1_1_1 1.01846 0.10256 9.93 0.0001 y1(t-1)
  AR1_1_2 -0.38682 0.09644 -4.01 0.0001 y2(t-1)
  MA1_1_1 0.32292 0.14524 2.22 0.0285 e1(t-1)
  MA1_1_2 -0.02160 0.14203 -0.15 0.8795 e2(t-1)
y2 AR1_2_1 0.39182 0.10062 3.89 0.0002 y1(t-1)
  AR1_2_2 0.55281 0.08422 6.56 0.0001 y2(t-1)
  MA1_2_1 -0.16501 0.15704 -1.05 0.2960 e1(t-1)
  MA1_2_2 0.58576 0.14115 4.15 0.0001 e2(t-1)

Covariance Parameter Estimates
Parameter Estimate Standard
Error 		t Value Pr > |t|
COV1_1 1.25202 0.17697 7.07 0.0001
COV1_2 0.37950 0.13401 2.83 0.0056
COV2_2 1.31315 0.18610 7.06 0.0001


The fitted VARMA(1,1) model with estimated standard errors in parentheses is given as

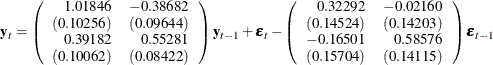
\begin{eqnarray*} \mb {y} _ t = \left( \begin{array}{rr} 1.01846 & -0.38682 \\ (0.10256)& (0.09644)\\ 0.39182 & 0.55281 \\ (0.10062)& (0.08422)\\ \end{array} \right) \mb {y} _{t-1} + \bepsilon _ t - \left( \begin{array}{rr} 0.32292 & -0.02160 \\ (0.14524)& (0.14203)\\ -0.16501 & 0.58576 \\ (0.15704)& (0.14115)\\ \end{array} \right) \bepsilon _{t-1} \end{eqnarray*}

and

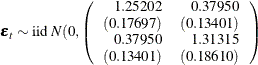
\begin{eqnarray*} \bepsilon _ t \sim \text {iid}\ N(0,\left( \begin{array}{rr} 1.25202 & 0.37950 \\ (0.17697)& (0.13401)\\ 0.37950 & 1.31315 \\ (0.13401)& (0.18610)\\ \end{array} \right) \end{eqnarray*}

VARMAX Modeling

A general VARMAX($p,q,s$) process is written as

\begin{eqnarray*} \mb {y} _{t} = \bdelta _ t + \sum _{i=1}^{p}\Phi _ i\mb {y} _{t-i} + \bepsilon _ t -\sum _{i=1}^{q} \Theta _ i\bepsilon _{t-i} \end{eqnarray*}

or

\begin{eqnarray*} \Phi (B)\mb {y} _{t} = \bdelta _ t + \Theta (B) \bepsilon _ t \end{eqnarray*}

where $\Phi (B) = I_ k - \sum _{i=1}^{p} \Phi _ i B^ i$, $\Theta (B) = I_ k - \sum _{i=1}^{q} \Theta _ i B^ i$. The $\bdelta _ t$ consists of all possible deterministic terms, namely constant, seasonal dummies, linear trend, quadratic trend, and exogenous variables; $\bdelta _ t = \Delta \mb {c}_ t$, where $\mb {c}_ t = (D_ t’\ \mb {x}_ t’\ \ldots \ \mb {x}_{t-s}’)’$; $D_ t = (1\ d_{t,1}\ \ldots \ d_{t,n_ s-1}\ t\ t^2)’$; $d_{t,i}, i=1, \ldots , n_ s-1$, are seasonal dummies and $n_ s$ is based on NSEASON= option; $\Delta = (A\ \Theta ^*_0\ \ldots \Theta ^*_ s)$; $A$ is the parameter matrix corresponding to $D_ t$ and $\Theta ^*_ i$ for $\mb {x}_{t-i},i=0, \ldots , s$.

The state-space form of the VARMAX($p$,$q$,$s$) model consists of a state equation

\[ \mb {z} _{t} =F\mb {z} _{t-1} + \mb {w}_ t + G\bepsilon _{t} \]

and an observation equation

\[ \mb {y} _ t = H\mb {z} _{t} \]

where for $v=\mr {max} (p,q+1)$

\[ \mb {z} _{t}=(\mb {y} _{t}’,\mb {y} _{t+1|t}’,\ldots ,\mb {y} _{t+v-1|t}’, \mb {c}_{t+v-1}’)’ \]
\[ \mb {w} _{t}=(0, \mb {c}_{t+v-1}’)’ \]
\[ F = \left[\begin{matrix} 0 & I_ k & 0 & {\cdots } & 0 & 0 \\ 0 & 0 & I_ k & {\cdots } & 0 & 0 \\ {\vdots } & {\vdots } & {\vdots } & \ddots & {\vdots } & 0 \\ \Phi _{v} & \Phi _{v-1} & \Phi _{v-2} & {\cdots } & \Phi _{1} & \Delta \\ 0 & 0 & 0 & {\cdots } & 0 & 0 \\ {\vdots } & {\vdots } & {\vdots } & \vdots & {\vdots } & {\vdots } \\ 0 & 0 & 0 & {\cdots } & 0 & 0 \\ \end{matrix} \right], ~ ~ G = \left[\begin{matrix} I_ k \\ \Psi _{1} \\ {\vdots } \\ \Psi _{v-1} \\ 0 \\ \end{matrix}\right] \]

and

\[ H = [I_ k, 0, \ldots , 0] \]

The Kalman filtering approach is used to evaluate the likelihood function. The updating equation is

\[ \hat{\mb {z}}_{t|t} = {\hat{\mb {z}}}_{t|t-1} + K_ t\bepsilon _{t|t-1} \]

where

\[ K_ t = P_{t|t-1}H’[H P_{t|t-1} H’]^{-1} \]

The prediction equation is

\[ \hat{\mb {z} }_{t|t-1} = F \hat{\mb {z} }_{t-1|t-1} + \mb {w}_ t, ~ ~ P_{t|t-1} = F P_{t-1|t-1} F’ + G \Sigma G’ \]

where $P_{t|t} = [I-K_ tH]P_{t|t-1}$ for $t=1,2,\ldots ,n$.

The log-likelihood function can be expressed as

\[ \ell = -\frac{1}{2} \sum _{t=1}^ T [ \log |\Sigma _{t|t-1}| + (\mb {y} _{t}-\hat{\mb {y} }_{t|t-1})’\Sigma _{t|t-1}^{-1} (\mb {y} _{t}-\hat{\mb {y} }_{t|t-1}) ] \]

where $\hat{\mb {y} }_{t|t-1}$ and $\Sigma _{t|t-1}$ are determined recursively from the Kalman filter procedure. To construct the likelihood function from Kalman filtering, you obtain $\hat{\mb {y} }_{t|t-1}=H \hat{\mb {z} }_{t|t-1}$, $\hat{\bepsilon }_{t|t-1} = \mb {y} _{t}-\hat{\mb {y} }_{t|t-1}$, and $\Sigma _{t|t-1}=H P_{t|t-1} H’$. Note that the dimension of the state-space vector of the Kalman filtering method for the VARMAX($p$,$q$,$s$) model is large, so it takes a lot of time and memory for computing.

Two examples of VARMAX modeling follow: 

model y1 y2 = x1 / q=1;
nloptions tech=qn;

model y1 y2 = x1 / p=1 q=1 xlag=1 nocurrentx;
nloptions tech=qn;
Previous Page|Next Page|Top of Page
Copyright © SAS Institute Inc. All Rights Reserved.