The VARMAX Procedure

Impulse Response Function

Subsections:

Simple Impulse Response Function (IMPULSE=SIMPLE Option)
Accumulated Impulse Response Function (IMPULSE=ACCUM Option)
Orthogonalized Impulse Response Function (IMPULSE=ORTH Option)
Impulse Response of Transfer Function (IMPULSX=SIMPLE Option)
Impulse Response of Transfer Function (IMPULSX=ACCUM Option)

Simple Impulse Response Function (IMPULSE=SIMPLE Option)

The VARMAX( $p$ , $q$ , $s$ ) model has a convergent representation

$\mb {y} _{t} = \Psi ^{*}(B)\mb {x} _{t} + \Psi (B) \bepsilon _{t}$

where $\Psi ^{*}(B)= \Phi (B)^{-1}\Theta ^{*}(B) =\sum _{j=0}^{\infty }\Psi _ j^{*} B^ j$ and $\Psi (B)=\Phi (B)^{-1}\Theta (B)=\sum _{j=0}^{\infty }\Psi _ j B^ j$ .

The elements of the matrices $\Psi _{j}$ from the operator $\Psi (B)$ , called the impulse response, can be interpreted as the impact that a shock in one variable has on another variable. Let $\psi _{j,in}$ be the $in^{th}$ element of $\Psi _ j$ at lag $j$ , where $i$ is the index for the impulse variable, and $n$ is the index for the response variable (impulse $\rightarrow$ response). For instance, $\psi _{j,11}$ is an impulse response to $y_{1t} \rightarrow y_{1t}$ , and $\psi _{j,12}$ is an impulse response to $y_{1t} \rightarrow y_{2t}$ .

Accumulated Impulse Response Function (IMPULSE=ACCUM Option)

The accumulated impulse response function is the cumulative sum of the impulse response function, $\Psi ^{a}_ l=\sum _{j=0}^{l}\Psi _ j$ .

Orthogonalized Impulse Response Function (IMPULSE=ORTH Option)

The MA representation of a VARMA( $p$ , $q$ ) model with a standardized white noise innovation process offers another way to interpret a VARMA( $p$ , $q$ ) model. Since $\Sigma$ is positive-definite, there is a lower triangular matrix $P$ such that $\Sigma =PP’$ . The alternate MA representation of a VARMA( $p$ , $q$ ) model is written as

$\mb {y} _{t} = \Psi ^{o}(B) \mb {u} _{t}$

where $\Psi ^{o}(B)=\sum _{j=0}^{\infty }\Psi ^{o}_ j B^ j$ , $\Psi ^{o}_ j=\Psi _ j P$ , and $\mb {u} _{t}=P^{-1}\bepsilon _ t$ .

The elements of the matrices $\Psi ^{o}_{j}$ , called the orthogonal impulse response, can be interpreted as the effects of the components of the standardized shock process $\mb {u} _ t$ on the process $\mb {y} _ t$ at lag $j$ .

Impulse Response of Transfer Function (IMPULSX=SIMPLE Option)

The coefficient matrix $\Psi _ j^{*}$ from the transfer function operator $\Psi ^{*}(B)$ can be interpreted as the effects that changes in the exogenous variables $\mb {x} _{t}$ have on the output variable $\mb {y} _{t}$ at lag $j$ ; it is called an impulse response matrix in the transfer function.

Impulse Response of Transfer Function (IMPULSX=ACCUM Option)

The accumulated impulse response in the transfer function is the cumulative sum of the impulse response in the transfer function, $\Psi ^{*a}_ l=\sum _{j=0}^{l}\Psi _ j^{*}$ .

The asymptotic distributions of the impulse functions can be seen in the section VAR and VARX Modeling.

The following statements provide the impulse response and the accumulated impulse response in the transfer function for a VARX(1,0) model.

proc varmax data=grunfeld plot=impulse;
   model y1-y3 = x1 x2 / p=1 lagmax=5
                         printform=univariate
                         print=(impulsx=(all) estimates);
run;

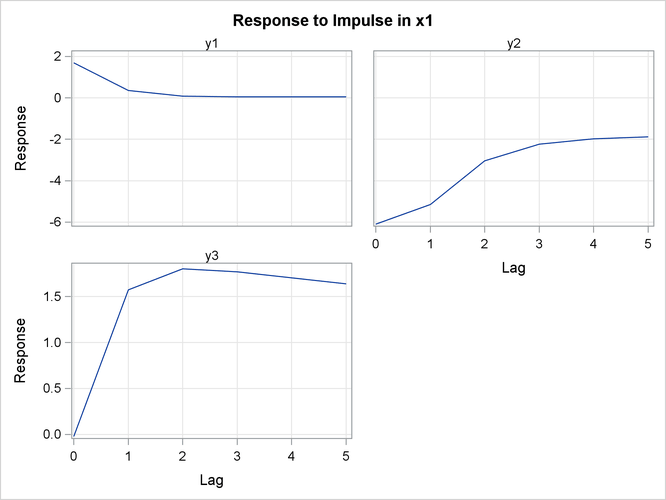
In Figure 35.26, the variables $x1$ and $x2$ are impulses and the variables $y1$ , $y2$ , and $y3$ are responses. You can read the table matching the pairs of $impulse \rightarrow response$ such as $x1 \rightarrow y1$ , $x1 \rightarrow y2$ , $x1 \rightarrow y3$ , $x2 \rightarrow y1$ , $x2 \rightarrow y2$ , and $x2 \rightarrow y3$ . In the pair of $x1 \rightarrow y1$ , you can see the long-run responses of $y1$ to an impulse in $x1$ (the values are 1.69281, 0.35399, 0.09090, and so on for lag 0, lag 1, lag 2, and so on, respectively).

Figure 35.26: Impulse Response in Transfer Function (IMPULSX= Option)

The VARMAX Procedure

Simple Impulse Response of Transfer Function by Variable
Variable Response\Impulse	Lag	x1	x2
y1	0	1.69281	-0.00859
	1	0.35399	0.01727
	2	0.09090	0.00714
	3	0.05136	0.00214
	4	0.04717	0.00072
	5	0.04620	0.00040
y2	0	-6.09850	2.57980
	1	-5.15484	0.45445
	2	-3.04168	0.04391
	3	-2.23797	-0.01376
	4	-1.98183	-0.01647
	5	-1.87415	-0.01453
y3	0	-0.02317	-0.01274
	1	1.57476	-0.01435
	2	1.80231	0.00398
	3	1.77024	0.01062
	4	1.70435	0.01197
	5	1.63913	0.01187

Figure 35.27 shows the responses of $y1$ , $y2$ , and $y3$ to a forecast error impulse in $x1$ .

Figure 35.27: Plot of Impulse Response in Transfer Function

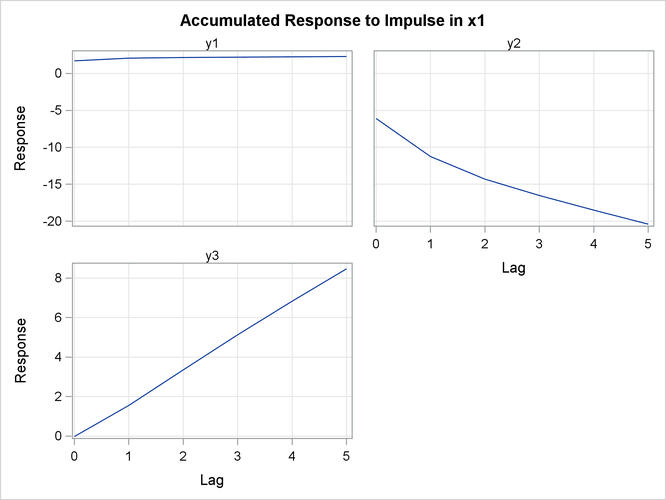
Figure 35.28 shows the accumulated impulse response in transfer function.

Figure 35.28: Accumulated Impulse Response in Transfer Function (IMPULSX= Option)

Accumulated Impulse Response of Transfer Function by Variable
Variable Response\Impulse	Lag	x1	x2
y1	0	1.69281	-0.00859
	1	2.04680	0.00868
	2	2.13770	0.01582
	3	2.18906	0.01796
	4	2.23623	0.01867
	5	2.28243	0.01907
y2	0	-6.09850	2.57980
	1	-11.25334	3.03425
	2	-14.29502	3.07816
	3	-16.53299	3.06440
	4	-18.51482	3.04793
	5	-20.38897	3.03340
y3	0	-0.02317	-0.01274
	1	1.55159	-0.02709
	2	3.35390	-0.02311
	3	5.12414	-0.01249
	4	6.82848	-0.00052
	5	8.46762	0.01135

Figure 35.29 shows the accumulated responses of $y1$ , $y2$ , and $y3$ to a forecast error impulse in $x1$ .

Figure 35.29: Plot of Accumulated Impulse Response in Transfer Function

The following statements provide the impulse response function, the accumulated impulse response function, and the orthogonalized impulse response function with their standard errors for a VAR(1) model. Parts of the VARMAX procedure output are shown in Figure 35.30, Figure 35.32, and Figure 35.34.

proc varmax data=simul1 plot=impulse;
   model y1 y2 / p=1 noint lagmax=5
                 print=(impulse=(all))
                 printform=univariate;
run;

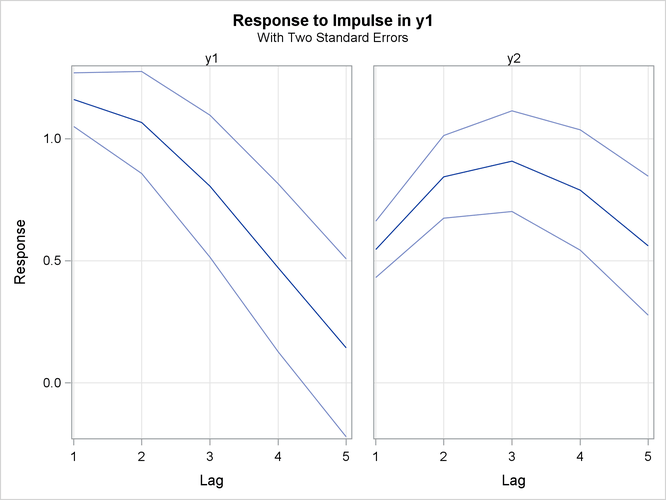
Figure 35.30 is the output in a univariate format associated with the PRINT=(IMPULSE=) option for the impulse response function. The keyword STD stands for the standard errors of the elements. The matrix in terms of the lag 0 does not print since it is the identity. In Figure 35.30, the variables $y1$ and $y2$ of the first row are impulses, and the variables $y1$ and $y2$ of the first column are responses. You can read the table matching the $impulse \rightarrow response$ pairs, such as $y1 \rightarrow y1$ , $y1 \rightarrow y2$ , $y2 \rightarrow y1$ , and $y2 \rightarrow y2$ . For example, in the pair of $y1 \rightarrow y1$ at lag 3, the response is 0.8055. This represents the impact on y1 of one-unit change in $y1$ after 3 periods. As the lag gets higher, you can see the long-run responses of $y1$ to an impulse in itself.

Figure 35.30: Impulse Response Function (IMPULSE= Option)

The VARMAX Procedure

Simple Impulse Response by Variable
Variable Response\Impulse	Lag	y1	y2
y1	1	1.15977	-0.51058
	STD	0.05508	0.05898
	2	1.06612	-0.78872
	STD	0.10450	0.10702
	3	0.80555	-0.84798
	STD	0.14522	0.14121
	4	0.47097	-0.73776
	STD	0.17191	0.15864
	5	0.14315	-0.52450
	STD	0.18214	0.16115
y2	1	0.54634	0.38499
	STD	0.05779	0.06188
	2	0.84396	-0.13073
	STD	0.08481	0.08556
	3	0.90738	-0.48124
	STD	0.10307	0.09865
	4	0.78943	-0.64856
	STD	0.12318	0.11661
	5	0.56123	-0.65275
	STD	0.14236	0.13482

Figure 35.31 shows the responses of $y1$ and $y2$ to a forecast error impulse in $y1$ with two standard errors.

Figure 35.31: Plot of Impulse Response

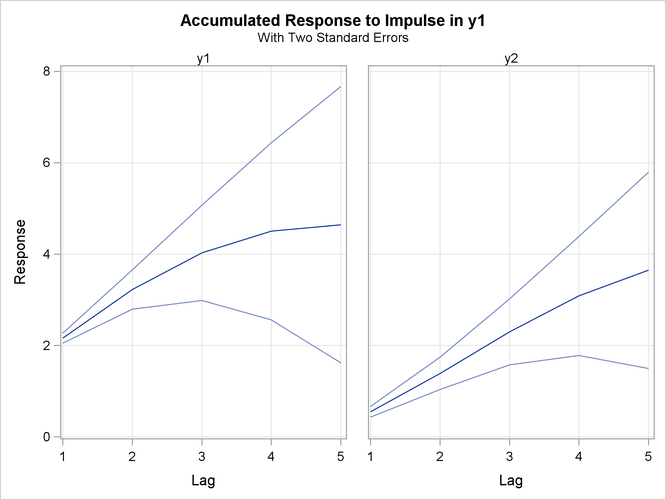
Figure 35.32 is the output in a univariate format associated with the PRINT=(IMPULSE=) option for the accumulated impulse response function. The matrix in terms of the lag 0 does not print since it is the identity.

Figure 35.32: Accumulated Impulse Response Function (IMPULSE= Option)

Accumulated Impulse Response by Variable
Variable Response\Impulse	Lag	y1	y2
y1	1	2.15977	-0.51058
	STD	0.05508	0.05898
	2	3.22589	-1.29929
	STD	0.21684	0.22776
	3	4.03144	-2.14728
	STD	0.52217	0.53649
	4	4.50241	-2.88504
	STD	0.96922	0.97088
	5	4.64556	-3.40953
	STD	1.51137	1.47122
y2	1	0.54634	1.38499
	STD	0.05779	0.06188
	2	1.39030	1.25426
	STD	0.17614	0.18392
	3	2.29768	0.77302
	STD	0.36166	0.36874
	4	3.08711	0.12447
	STD	0.65129	0.65333
	5	3.64834	-0.52829
	STD	1.07510	1.06309

Figure 35.33 shows the accumulated responses of $y1$ and $y2$ to a forecast error impulse in $y1$ with two standard errors.

Figure 35.33: Plot of Accumulated Impulse Response

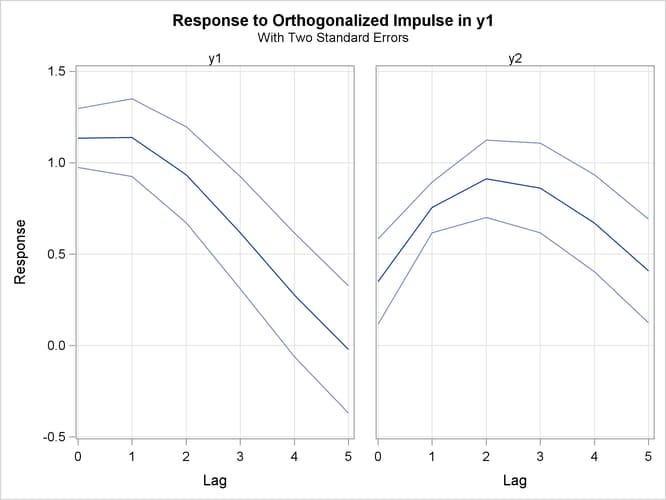
Figure 35.34 is the output in a univariate format associated with the PRINT=(IMPULSE=) option for the orthogonalized impulse response function. The two right-hand side columns, $y1$ and $y2$ , represent the $y1\_ innovation$ and $y2\_ innovation$ variables. These are the impulses variables. The left-hand side column contains responses variables, $y1$ and $y2$ . You can read the table by matching the $impulse \rightarrow response$ pairs such as $y1\_ innovation \rightarrow y1$ , $y1\_ innovation \rightarrow y2$ , $y2\_ innovation \rightarrow y1$ , and $y2\_ innovation \rightarrow y2$ .

Figure 35.34: Orthogonalized Impulse Response Function (IMPULSE= Option)

Orthogonalized Impulse Response by Variable
Variable Response\Impulse	Lag	y1	y2
y1	0	1.13523	0.00000
	STD	0.08068	0.00000
	1	1.13783	-0.58120
	STD	0.10666	0.14110
	2	0.93412	-0.89782
	STD	0.13113	0.16776
	3	0.61756	-0.96528
	STD	0.15348	0.18595
	4	0.27633	-0.83981
	STD	0.16940	0.19230
	5	-0.02115	-0.59705
	STD	0.17432	0.18830
y2	0	0.35016	1.13832
	STD	0.11676	0.08855
	1	0.75503	0.43824
	STD	0.06949	0.10937
	2	0.91231	-0.14881
	STD	0.10553	0.13565
	3	0.86158	-0.54780
	STD	0.12266	0.14825
	4	0.66909	-0.73827
	STD	0.13305	0.15846
	5	0.40856	-0.74304
	STD	0.14189	0.16765

In Figure 35.4, there is a positive correlation between $\varepsilon _{1t}$ and $\varepsilon _{2t}$ . Therefore, shock in $y1$ can be accompanied by a shock in $y2$ in the same period. For example, in the pair of $y1\_ innovation \rightarrow y2$ , you can see the long-run responses of $y2$ to an impulse in $y1\_ innovation$ .

Figure 35.35 shows the orthogonalized responses of $y1$ and $y2$ to a forecast error impulse in $y1$ with two standard errors.

Figure 35.35: Plot of Orthogonalized Impulse Response