The COUNTREG Procedure

Zero-Inflated Conway-Maxwell-Poisson Regression

Subsections:

Zero-Inflated Conway-Maxwell-Poisson Model with Logistic Link Function
Zero-Inflated Conway-Maxwell-Poisson Model with Normal Link Function

In the Conway-Maxwell-Poisson regression model, the data generation process is defined as

$P(Y_{i}=y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = \frac{1}{Z(\lambda _{i},\nu _{i})} \frac{\lambda _{i}^{y_{i}}}{(y_{i}!)^{\nu _{i}}}, \quad y_ i = 0,1,2,\ldots$

where the normalization factor is

$Z(\lambda _ i,\nu _ i) = \sum _{n=0}^{\infty }\frac{\lambda _{i}^{n}}{(n!)^{\nu _{i}}}$

and

$\lambda _{i} = \exp (\mathbf{x}_{i}^{\prime } \bbeta )$

$\nu _{i}=-\exp (\mathbf{g}_{i}^{\prime } \delta )$

The zero-inflated Conway-Maxwell-Poisson model can be written as

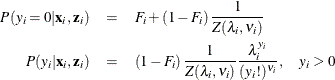
$\begin{eqnarray*} P(y_{i}=0|\mathbf{x}_{i},\mathbf{z}_{i}) & =& F_{i} + \left(1 - F_{i}\right)\frac{1}{Z(\lambda _{i},\nu _{i})} \\ P(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) & =& \left(1- F_{i} \right)\frac{1}{Z(\lambda _{i},\nu _{i})} \frac{\lambda _{i}^{y_{i}}}{(y_{i}!)^{\nu _{i}}}, \quad y_{i}>0 \end{eqnarray*}$

The conditional expectation and conditional variance of $y_{i}$ are given by

$E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = (1 -F_{i})\frac{1}{Z(\lambda ,\nu )} \sum _{j=0}^{\infty }\frac{j \lambda ^{j}}{(j!)^{\nu }}$

$V(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = (1 -F_{i})\frac{1}{Z(\lambda ,\nu )} \sum _{j=0}^{\infty }\frac{j^{2} \lambda ^{j}}{(j!)^{\nu }}-E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i})^2$

General form of the log-likelihood function for the Conway-Maxwell-Poisson zero-inflated model is

$\mathcal{L} = \sum _{i=1}^{N}w_ i\ln \left[ P(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) \right]$

Zero-Inflated Conway-Maxwell-Poisson Model with Logistic Link Function

In this model the probability $\varphi _{i}$ is expressed with a logistic link function as

$\varphi _{i}=\Lambda (\mathbf{z}_{i}’\bgamma )=\frac{\exp (\mathbf{z}_{i}\bgamma )}{1+\exp (\mathbf{z}_{i}\bgamma )}$

The log-likelihood function is

$\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} }w_ i\ln \left\{ \Lambda (\mathbf{z}_{i}’\bgamma ) + \left[ 1- \Lambda (\mathbf{z}_{i}’\bgamma )\right] \frac{1}{Z(\lambda _{i},\nu _{i})} \right\} \\ & + & \sum _{\{ i: y_{i}>0\} }w_ i\left\{ \ln \left[ \left( 1-\Lambda (\mathbf{z}_{i}’\bgamma )\right) \right] - ln(Z(\lambda ,\nu )) + (y_{i}\ln (\lambda ) - \nu \ln (y_ i!) \right\} \end{eqnarray*}$

Zero-Inflated Conway-Maxwell-Poisson Model with Normal Link Function

For this model, the probability $\varphi _{i}$ is specified with the standard normal distribution function (probit function): $\varphi _{i}= \Phi (\mathbf{z}_{i}’\bgamma )$ .

The log-likelihood function is written as

$\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} }w_ i\ln \left\{ \Phi (\mathbf{z}_{i}’\bgamma ) + \left[ 1- \Phi (\mathbf{z}_{i}’\bgamma )\right] \frac{1}{Z(\lambda _{i},\nu _{i})} \right\} \\ & + & \sum _{\{ i: y_{i}>0\} }w_ i\left\{ \ln \left[ \left( 1-\Phi (\mathbf{z}_{i}’\bgamma )\right) \right] - ln(Z(\lambda ,\nu )) + (y_{i}\ln (\lambda ) - \nu \ln (y_ i!) \right\} \end{eqnarray*}$