The ARIMA Procedure
- Overview
-
Getting Started
The Three Stages of ARIMA ModelingIdentification StageEstimation and Diagnostic Checking StageForecasting StageUsing ARIMA Procedure StatementsGeneral Notation for ARIMA ModelsStationarityDifferencingSubset, Seasonal, and Factored ARMA ModelsInput Variables and Regression with ARMA ErrorsIntervention Models and Interrupted Time SeriesRational Transfer Functions and Distributed Lag ModelsForecasting with Input VariablesData Requirements -
Syntax
-
DetailsThe Inverse Autocorrelation FunctionThe Partial Autocorrelation FunctionThe Cross-Correlation FunctionThe ESACF MethodThe MINIC MethodThe SCAN MethodStationarity TestsPrewhiteningIdentifying Transfer Function ModelsMissing Values and AutocorrelationsEstimation DetailsSpecifying Inputs and Transfer FunctionsInitial ValuesStationarity and InvertibilityNaming of Model ParametersMissing Values and Estimation and ForecastingForecasting DetailsForecasting Log Transformed DataSpecifying Series PeriodicityDetecting OutliersOUT= Data SetOUTCOV= Data SetOUTEST= Data SetOUTMODEL= SAS Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesStatistical Graphics
-
Examples
- References
The ARIMA procedure produces printed output for each of the IDENTIFY, ESTIMATE, and FORECAST statements. The output produced by each ARIMA statement is described in the following sections.
The printed output of the IDENTIFY statement consists of the following:
-
a table of summary statistics, including the name of the response variable, any specified periods of differencing, the mean and standard deviation of the response series after differencing, and the number of observations after differencing
-
a plot of the sample autocorrelation function for lags up to and including the NLAG= option value. Standard errors of the autocorrelations also appear to the right of the autocorrelation plot if the value of LINESIZE= option is sufficiently large. The standard errors are derived using Bartlett’s approximation (Box and Jenkins 1976, p. 177). The approximation for a standard error for the estimated autocorrelation function at lag k is based on a null hypothesis that a pure moving-average Gaussian process of order k–1 generated the time series. The relative position of an approximate 95% confidence interval under this null hypothesis is indicated by the dots in the plot, while the asterisks represent the relative magnitude of the autocorrelation value.
-
a plot of the sample inverse autocorrelation function. See the section The Inverse Autocorrelation Function for more information about the inverse autocorrelation function.
-
a plot of the sample partial autocorrelation function
-
a table of test statistics for the hypothesis that the series is white noise. These test statistics are the same as the tests for white noise residuals produced by the ESTIMATE statement and are described in the section Estimation Details.
-
a plot of the sample cross-correlation function for each series specified in the CROSSCORR= option. If a model was previously estimated for a variable in the CROSSCORR= list, the cross-correlations for that series are computed for the prewhitened input and response series. For each input variable with a prewhitening filter, the cross-correlation report for the input series includes the following:
-
a table of test statistics for the hypothesis of no cross-correlation between the input and response series
-
the prewhitening filter used for the prewhitening transformation of the predictor and response variables
-
-
ESACF tables if the ESACF option is used
-
MINIC table if the MINIC option is used
-
SCAN table if the SCAN option is used
-
STATIONARITY test results if the STATIONARITY option is used
The printed output of the ESTIMATE statement consists of the following:
-
if the PRINTALL option is specified, the preliminary parameter estimates and an iteration history that shows the sequence of parameter estimates tried during the fitting process
-
a table of parameter estimates that show the following for each parameter: the parameter name, the parameter estimate, the approximate standard error, t value, approximate probability (
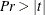), the lag for the parameter, the input variable name for the parameter, and the lag or “Shift” for the input variable
-
the estimates of the constant term, the innovation variance (variance estimate), the innovation standard deviation (Std Error Estimate), Akaike’s information criterion (AIC), Schwarz’s Bayesian criterion (SBC), and the number of residuals
-
the correlation matrix of the parameter estimates
-
a table of test statistics for hypothesis that the residuals of the model are white noise. The table is titled “Autocorrelation Check of Residuals.”
-
if the PLOT option is specified, autocorrelation, inverse autocorrelation, and partial autocorrelation function plots of the residuals
-
if an INPUT variable has been modeled in such a way that prewhitening is performed in the IDENTIFY step, a table of test statistics titled “Crosscorrelation Check of Residuals.” The test statistic is based on the chi-square approximation suggested by Box and Jenkins (1976, pp. 395–396). The cross-correlation function is computed by using the residuals from the model as one series and the prewhitened input variable as the other series.
-
if the GRID option is specified, the sum-of-squares or likelihood surface over a grid of parameter values near the final estimates
-
a summary of the estimated model that shows the autoregressive factors, moving-average factors, and transfer function factors in backshift notation with the estimated parameter values.
The printed output of the OUTLIER statement consists of the following:
-
a summary that contains the information about the maximum number of outliers searched, the number of outliers actually detected, and the significance level used in the outlier detection.
-
a table that contains the results of the outlier detection process. The outliers are listed in the order in which they are found. This table contains the following columns:
-
The Obs column contains the observation number of the start of the level shift.
-
If an ID= option is specified, then the Time ID column contains the time identification labels of the start of the outlier.
-
The Type column lists the type of the outlier.
-
The Estimate column contains
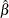, the estimate of the regression coefficient of the shock signature.
-
The Chi-Square column lists the value of the test statistic
.
-
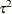The Approx Prob > ChiSq column lists the approximate p-value of the test statistic.
-
The printed output of the FORECAST statement consists of the following:
-
a summary of the estimated model
-
a table of forecasts with following columns:
-
The Obs column contains the observation number.
-
The Forecast column contains the forecast values.
-
The Std Error column contains the forecast standard errors.
-
The Lower and Uppers columns contain the approximate 95% confidence limits. The ALPHA= option can be used to change the confidence interval for forecasts.
-
If the PRINTALL option is specified, the forecast table also includes columns for the actual values of the response series (Actual) and the residual values (Residual).
-